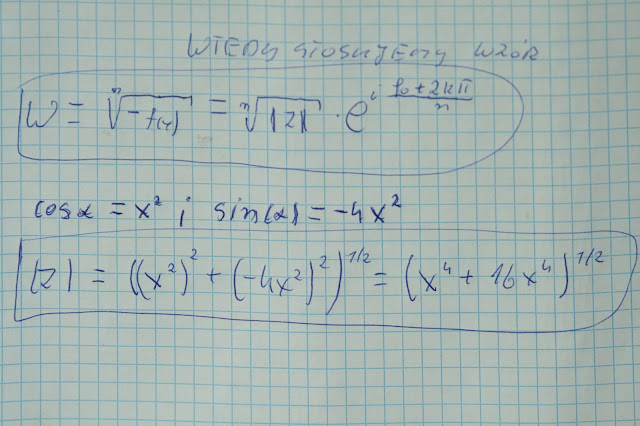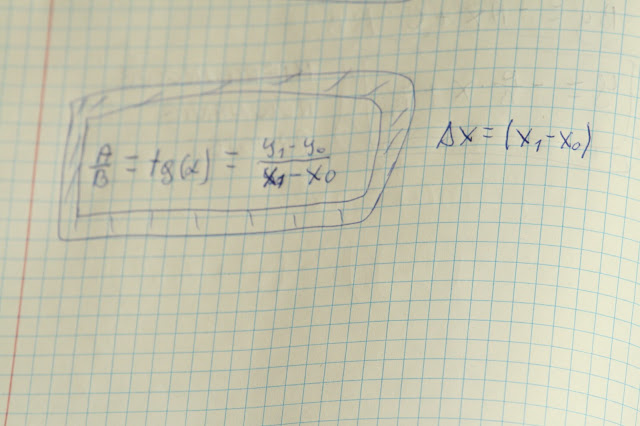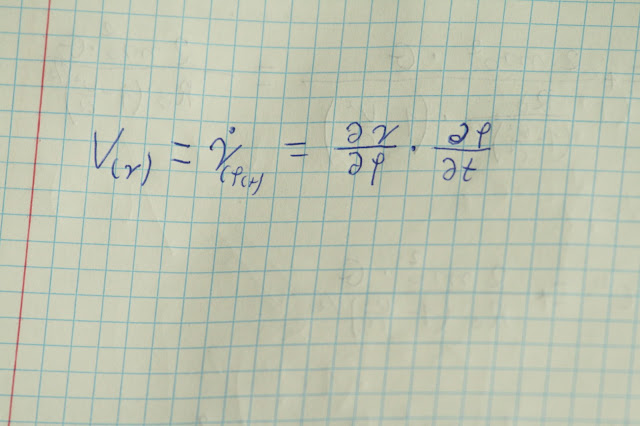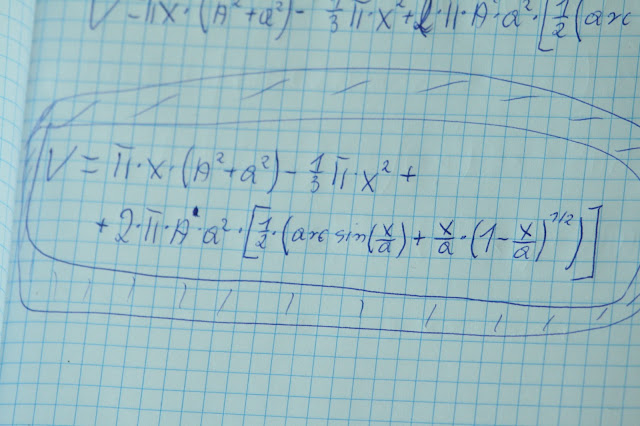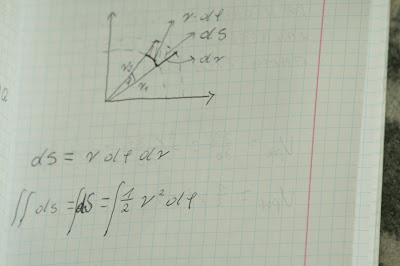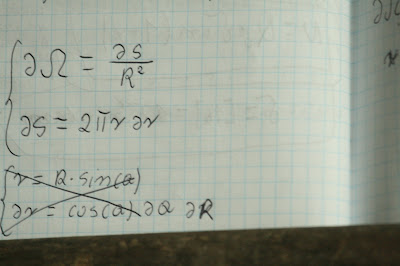Podstawy matematyki - Rachunek Różniczkowy - Wykład- Równanie różniczkowe pierwszego stopnia - Rzut ukośny z oporem powietrza - Siła nośna samolotu

                                             Ogólny wzór na liczenie tensorów.

Wstęp

Kto dopiero zaczyna naukę matematyki, lub ma poważne trudności ze zrozumieniem tego bloga,dobrze trafił. Żeby módz żąglować wzorami, potrzebne są pewne aksjomaty, co w przełożeniu na nasze, oznacza podstawy, których nie trzeba udowadniać, które po prostu są gdyż taka jest natura rzeczy. Takich podstaw nie jest dużo, w porównaniu do korzyści jakie odniesiemy z ich znajomości, opłaca się włożyć co prawda nie mały wysiłek w ich naukę. Proponujemy wykonać dużo działań na tych podstawach, tak by zapadły w pamięć i pod świadomość, dopiero później można ruszyć dalej. 

Rozwój czakr ziemskich powinien iść w parze z rozwojem czakr duchowych, i dla nich istnieją podstawowe aksjomaty, które należy w tym przypadku zrozumieć. Dlatego polecamy na wstępie przeczytać też poniższy artykuł

http://jakpowstajfraktale.blogspot.com/2012/03/podstawowe-zasady-dobra.html

http://jakpowstajfraktale.blogspot.com/2012/03/czakry-czakramy-rownania-miosci.html

Prawa aksjomatyczne to prawa, które niepodlegają dowodzeniu. Wobec tego prawa te należy nauczyć się na pamięć. Mówiąc dosadnie wkuć je tak by umieć w nocy o północy, by zapadły w pod świadomość. Bez zapamiętania tych aksjomatów droga do matematyki i innych przedmiotów ścisłych jest zamknięta. Do kompletu należy jeszcze zapamiętać wzory na upraszczanie skomplikowanych funkcji, które znajdziecie tutaj

http://jakpowstajfraktale.blogspot.com/2012/05/szereg-maclarena-furiera-podstawowe.html

i można zgłębiać tajniki matematyki wyższej.

Podstawowy aksjomat sprowadzania do wspólnego mianownika

Przykład

To naszym zdaniem najważniejszy aksjomat. Bez niego nie można by było upraszczać równań. Nie można też by było w większości przypadków wyliczać niewiadomych z tych równań

                  Aksjomat dzielenia ułamka przez ułamek

Podzielić ułamek przez ułamek to to samo co pomnożyć pierwszy ułamek przez odwrotność drugiego

Na powyższym zdjęciu jest szkolny błąd, którego niezauważyliśmy. To dowód jak bardzo zły nas kontroluje. Tym samym Wy ucząc się matematyki będziecie narażeni na jego ataki. Poprawny wynik, który dodaliśmy po paru dniach od powstania tego artykułu pokazaliśmy na zjęciu poniżej.

Aksjomaty funkcji trygonometrycznych

Są to wprowadzone wielkości opisujące trójkąt, które potwierdzono doświadczalnie. To też aksjomaty i trzeba nauczyć się ich na pamięć.

To że suma kwadratów sinusa i kosinusa równa jest jeden, Wielokrotnie potwierdzono doświadczalnie i takie doświadczenie każdy sam może sobie przeprowadzić mierząc trójkąty o różnych bokach a i b. Mając dwa trzy udowodnione równania, można już przeprowadzać na nich kolejne kombinacje. Pokażemy tu jedną. 

Wyrazimy tg za pomocą kosinusa

Aksjomaty działań na równaniach znajdują się niżej. Są bardzo ważne.

Aksjomaty działań na równaniach

Na równaniach możemy wykonywać następujące operacje

1

Przenosić całe wyrażenia lub liczby pojedyncze z jednej strony na drugą ze zmienionym znakiem

Przykład przeprowadzimy na samych liczbach. Rozpatrzmy takie równanie

                                                 2+2 = 4

Jest ono prawdziwe, gdyż lewa strona równa się prawej. Przenieśmy teraz zgodnie z tą zasadą dwójkę na prawą stronę

                                                  2 = 4 - 2

                                                   2 = 2

Po takiej operacji też otrzymaliśmy prawdziwe równanie, prawa strona równa się lewej

2

Obustronnie mnożyć równanie przez tą samą liczbę

3

Obustronnie dzielić równanie przez tą samą liczbę

4

Obustronnie podnosić równanie do tej samej potęgi

5 

Wyciągać przed nawias wspólny czynnik Np.

2*x^2 -3*x = 5

Wspólnym czynnikiem jest x wtedy

x*(2*x - 3) = 2

Po wymnożeniu nawiasu otrzymamy poprzednią postać równania,

Czyli dokonaliśmy operacji upraszczającej to równanie a nie zmieniającej.

5

Obustronnie logarytmować równanie przez ten sam logarytm

Przykład

Dowód

W tym przykładzie dodaliśmy i jednocześnie odjęliśmy y. Wykorzystałem następujący aksjomat

Oraz aksjomat wyłączania wspólnego czynnika przed nawias, którym w podanym przykładzie jest x^2.

W paru słowach płęta. Możemy wykonywać na równaniach takie działania by równanie którego lewa strona równała się prawej ( w przeciwnym przypadku równanie jest fałszywe np. da wynik 2 =3 co jest widoczną nieprawdą), po zadziałaniu na niego w wyżej opisany sposób dalej było prawdziwe, to znaczy by dało wynik np. 2 =2. Trzeba przede wszystkim nauczyć się tych aksjomatów, gdyż gwarantują one prawdziwość równań, przed i po operacji na nich

Przykład

                                                 Aksjomaty potęg

                                               Aksjomaty logarytmów

 Logarytm jest odwrotnością funkcji 

                                                       c= a^b

wprowadzono więc  na tej podstawie funkcję zwaną logarytmem, taką, że

                                     b = loga(c)

funkcja o podstawie e, która jest liczbą równą 

                                    e = 2,781,,,,, 

Występuje tak często w matematyce, że nadano jej specjalny symbol

                                      loge = ln

Liczby a i e nazywamy podstawą logarytmu.

Poniższe zdjęcie pokazuje opracje na logarytmach, ich tożsamości i jak wyżej wspomnieliśmy trzeba nauczyć się ich na pamięć

Po przez ln występujący na zdjęciu rozumiemy log o podstawie a i b, Zrobiliśmy to po to by się przyzwyczaić do oznaczenia ln jest to wyjątkowy logarytm po przez bardzo częste występowanie. 

Znając te aksjomaty możemy udowodnić działania na potęgach

Logarytmy typu log o podstawie a występują w matematyce i w fizyce sporadycznie.

Liczby a, b i c są dowolnymi liczbami. tylko symbol e jest zarezerwowany dla liczby 2,781....

To samo tyczy się liczb zespolonych gdzie liczba urojona (i) podniesiona do kwadratu daje -1, a którą wprowadzono aksjomatycznie. We wszystkich pozostałych przypadkach ujemna liczba podniesiona do kwadratu daje liczbę dodatnią. 

Sama liczba (i) nie ma wartości liczbowej, dopiero jej kwadrat daje -1. Moduły we wzorach, w których występuje (i), nie bierzemy pod uwagę, jednak zostawiamy te moduły gdyż w dalszych podstawieniach, do innych wzorów (i) może wystąpić w kwadracie, co da jej wartość -1. Np.

                              y = a*x +i^2*x^2  = a*x+(-1)*x^2 = a*x - x^2

Po podstawieniu iksa wynikiem liczbowym takiej funkcji jest tylko moduł a*x

Liczbie zespolonej nadano symbol 

                                             Z = a - i*b

Została wprowadzona aksjomatycznie, gdyż zaobserwowano w przyrodzie zjawiska, które znikają w przewidujących je równaniach, a pozostają tylko wtedy gdy wprowadzi się liczbę urojoną (i).

Znak minus wprowadzono po to by uzyskać płaszczyznę zespoloną.

Łatwo sprawdzić, że liczba sprzężona do liczby zespolonej równa

                                              Z* = a+i*b

Która też została wprowadzona aksjomatycznie

 do liczby zespolonej, razy liczba zespolona daje  

                          Z x Z* =  a^2 + b^2 = R^2

A ponieważ jest to twierdzenie Pitagorasa więc wielkość ta równa się R^2 czyli promieniowi okręgu na płaszczyźnie.

Na osi y zaznaczamy a , zaś na osi x zaznaczamy i*b,tak jak pokazaliśmy na poniższym zdjęciu.

Kolejnym wzorem wprowadzonym aksjomatycznie dla liczb zespolonych jest wzór pokazany niżej

Jest to najprawdopodobniej aksjomat, trzeba nauczyć się go na pamięć.

na powyższym zdjęciu sinus i kosinus powinny być w nawiasie, przepraszamy za błąd.

                                                Twierdzenie More"a

                                               Przykład

                                               Twierdzenie

Itstneje dokładnie n pierwiastków liczby pod pierwiastkiem stopnia n, i wyrażają się one wzorem :

Należy jeszcze dodać, że moduł liczby z jest wartością bezwzględną więc zawsze dodatnią

                                                 Przykład

Każdą liczbę można przedstawić za pomocą pierwiastka

Wyraźnie widać, że ten wzór stanowi nadbudowę do rozwiązania równań kwadratowych a ogólnie n - tego stopnia, gdy n jest całkowite dodatnie, tu mamy uzupełnienie o potęgi ułamkowe.

Bardzo potężny wzór

Trzeba się po prostu nauczyć tego na pamięć, to tylko parę wzorów na Z i Z*, cała reszta wynika z logicznych zależności

Trzeba się po prostu nauczyć tego na pamięć, to tylko dwa wzory na Z i Z*, cała reszta wynika z logicznych zależności

Załóżmy teraz, że opisujemy matematycznie jakieś zjawisko i wyszedł nam trój mian kwadratowy, którego delta jest mniejsza od zera. Oznacza to, że nie ma rozwiązania takiego trójmianu, jednak w przyrodzie występuje takie zjawisko, co wtedy robić. Wzoru jesteśmy pewni. Przykład podajemy na poniższych zdjęciach

Pamiętamy, że 

e^(i*fi) = cos(fi) + i*sin(fi)

Co w połączeniu ze wzorami

Daje kompletne rozwiązanie. sinus plus kosinus wstawiamy za e^(i*fi), a f(x) jest naszą funkcją, która nie dała rozwiązania w dziedzinie liczb rzeczywistych. 

Daje kompletne rozwiązanie. sinus plus kosinus wstawiamy za e^(i*fi), a f(x) jest naszą funkcją, która nie dała rozwiązania w dziedzinie liczb rzeczywistych. d(f(x))/d(x) - jest pochodną tej funkcji, żeby się dowiedzieć o pochodnych zapraszm na naszą stronę

www.latwa-matematyka.blogspot.com

Części urojonej, to znaczy części wzoru w którym występuje czynnik (i) nie bierzemy pod uwagę. Rozwiązaniem jest tylko część rzeczywista, jednak części urojonej nie odrzucamy przy dalszych podstawieniach do innych wzorów. Podstawiamy cały wzór.

ASJOMATY DZIAŁAŃ NA WEKTORACH

Też trzeba nauczyć się na pamięć. Podaliśmy tu wzory na sumę iloczyn długość sinus konta alfa i kosinus między wektorami.

Aksjomat mnożenia wektora przez wektor jest dziwnym co najmniej aksjomatem.

a+b wcale nie równa się a*b, gdzie za a i b podstawiamy dowolne liczby. tym samym można go traktować jako przybliżenie, choć ja znam lepsze. Oto oto ono

Moim zdaniem powinno być

Poniżej zamieszczam wykres dla 

a = [3 ; 2]

b = [4 ; 3]

Podałem błędny wynik powinno być 12,04. Przepraszam za błąd.

To potraktujcie jako ciekawostkę nie radzę podawać go jako prawdziwe na kolokwiach czy klasówkach gdyż wrócicie z dwóją

MOŻECIE TERAZ PRZECZYTAĆ ARTYKUŁ - BŁĄD WSZECHŚWIATA.

tym samym wzory podanie niżej na sin i cos pomiędzy dwoma wektorami, trzba by było uzupełnić o podaną wyżej zależność

My proponujemy rozwiązać następujący układ równań

Zauważmy, że tangensy są pochodnymi funkcji liniowej przedstawiającej wektory a i b i nie tylko liniowej lecz wszystkich funkcji. W ten sposób otrzymujemy wzór na cosinus konta między dwiema dowolnymi funkcjami. Z wyprowadzeniem sinusa sami już sobie poradzicie. Ogólny zapis wygląda następująco

Rachunek pochodnych znajdziecie tutaj

http//jakpowstajfraktale.blogspot.com

Dalej będziemy posługiwać się wzorami oficjalnie przyjętymi

Wzory aksjomatyczne  na sinus i kosinus między osią x

Tu taj wzory na kosinus i sinus tyczą się kąta między osią x

   Wzory na sinus i kosinus między dwoma wektorami

We wzorze na cos, powinno być

a1*b2 + a2*b1

Jednak należy pamiętać, że wzór na cosinus przyjęty przez oficjalną naukę jest w formie podanej na zdjęciu poniżej.

                           Twierdzenie kosinusów

Dotyczy ono sytuacji gdy mamy trzy wektory, Tak jak pokazano na poniższym zdjęciu.

By twierdzenie było prawdziwe, wektory a i b muszą być skierowane przeciwnie do siebie, tak jak poazałem na powyższym zdjęciu. Zachodzi wtedy równość 

                                              c = a-b

Stąd c^2

Koniecznie musi być spełniony warunek c = a-b!!!!!!!!!!!!!!!!!

Jeżeli nie jest nie wolno stosować tego wzoru.

Koniec aksjomatów, chyba podałem wszystkie najbardziej podstawowe. Teraz skorzystamy z nich by wyprowadzić ogólne i kierunkowe równanie prostej.

Do ogólnego równania prostej dochodzimy startując z definicji kosinusa między wektorami. Z kosinusa dlatego by dwa wektory miały część wspólną, bu przecinały się ze sobą. Zakładamy warunek początkowy taki, że dwa wektory są do siebie, to oznacza kont prostopadłe, zauważmy, że taki warunek oznacza kąt równy 90 stopni a to z kolei pociąga za sobą fakt iż cos(90) = 0

Nigdy nie wolno dzielić przez zero gdyż taki cosinus ma granicę niewłaściwą w nieskończoności. Dlatego licznik przyrównujemy do zera

Sporządzimy sobie następujący schemat

Zakładamy, że współrzędne x0 i y0 są znane oraz znane są współrzędne A i B.  Wektor delta(P) ma współrzędne

                         delta(P) = [(x-xo) ; (y-y0)] = [b1 ; b2]

i odpowiednio A = a1 i B = a2

Podstawiamy to do pierwszego równania otrzymanego z definicji kosinusa

Ponieważ xo i yo są punktami zaczepienia znanymi więc

A*xo-B*yo = c stałej. Stąd ogólne równanie prostej przechodzącej przez punkt o współrzędnych [A ; B] ma postać

                        Jest to Ogólne Równanie Prostej.

W ten sposób nierozerwalnie połączyliśmy ze sobą prostą i punkt (a). Ponieważ założyliśmy cos = 0 więc mamy pewność, że punkt a leży na prostej wyznaczonej przez dwa punkty, którym drugim punktem jest punkt P.

                             Kierunkowe równanie prostej

Otrzymujemy przez zwykłe rozwiązanie równania względem y

Jeżeli teraz będziemy zmieniać A,B x i y, będziemy tym samym obracać wektor P a więc i prostą na której leży. Po rozwiązaniu względem y otrzymujemy kierunkowe równanie prostej

a zmiana delta(y) która wynika ze zmiany A;B y i x wynosi

Z podanych wyżej wykresów możemy napisać równość

Wstawiając to do równania na delta(y) i pamiętając, że delta(y) = y - yo najogólniej, otrzymamy 

Jest to równanie kierunkowe prostej

Powtórzymy tą czynność jeszcze ra, to znaczy znowu zmieniamy x a co za tym idzie zmienia się i y. Możemy więc napisać

Stąd już tylko krok do pochodnej

                            Rachunek różniczkowy - Pochodna

Do definicji różniczki dochodzimy startując z definicji pochodnej funkcji w punkcie, lub inaczej zwanej granicą ilorazu różnicowego. Cym jest ten iloraz różnicowy?

Jak sama nazwa wskazuje jest czegoś różnicą, a iloraz inaczej na zywamy dzieleniem.

Otóż jest to różnica dowolnej funkcji po dodaniu do niej bardzo małego przyrostu i przed dodaniem do niej tego przyrostu

Jeżeli przykładowo mamy funkcję 

f(x) = x^2

To 

delta(f(x)) = (x+delta(x))^2

Po prostu do x- sa dodajemy bardzo mały przyrost, który oznaczono 

delta(x) = (x1 - x2). 

Dalej wszystko się wyjaśni.

Pokażemy to na przykładzie funkcji kwadratowej, którą przedstawiliśmy na poniższym rysunku.

Otóż gdy zmierzamy z delta x do punktu a=x, wtedy i delta f(x) zmierza do pewnej wartości f(a), a sama różnica 

delta f(x)=f(x2)-f(x1) = f(x+delta(x))

 zmierza do zera. Patrz na poniższy rysunek.

delta x jest właśnie tym małym przyrostemlub ściśle bardzo małą zmianą, tórej odpowiada bardzo mała zmiana fx.

Gdy mamy funkcję f(x), to jak już wcześniej powiedzieliśmy, dodajemy do niej delta x, ten bardzo mały przyrost.

Więc nasza różnica delta f(x) wygląda tak jak na poniższym zdjęciu.

To ciężka granica do policzenia. Ten przykład daliśmy po to by sobie uzmysłowić, że wzory na pochodne poszczególnych funkcji rodziły się w bulach. Powyższy ciąg logiczny prowadzi do sprzeczności. Stosując inny ciąg logiczny, którego nie znamy udowodniono, że granicą jest jeden.

Aksjomatycznie pochodną ze stałej przyjęto równą zero. Popełniłem błąd logiczny, gdy do stałej dodamy delta x wtedy delta y = y, wykresem jest linia pozioma dlatego pochodna ze stałej równa się zeru.

Ostatecznie obarczenie błędem każdego towaru dane jest wzorem.

Udowodnimy teraz czemu równa jest pochodna funkcji złożonej typu

Y = f(x)*g(x)

Dowód logiczny stu procentowy

Dodamy jeszcze, że stu procentowy dowód logiczny nie stanowi ogólnego dowodu, gdyż samą logiką możemy zawędrować w ślepy zaułek. ogólny dowód to dowód logiczny + doświadczalny

Więcej takich wyprowadzeń wzorów znajdziecie tutaj

http://jakpowstajfraktale.blogspot.com/2012_05_01_archive.html

Są bardziej skomplikowane , a ten artykuł przeznaczony jest przecież dla początkujących dlatego umieściliśmy go osobno.

   Pochodne drugiego i n -teg stopnia

                                              Interpretacja geometryczna pochodnej

Ta interpretacja jest tak prosta, że czytelnicy mogą czuć się zawiedzeni. Otóż z trygonometrii wiadomo, że delta(y)/delta(x) jest definicją tg(afa), a dodając granicę jak wyżej przedstawiono otrzymujemy pochodną w punkcie. Tak więc dochodzimy do bardzo ważnego i potężnego wniosku

                                              Pochodna funkcji f(x) = tg(alfa)

Więcej znajdziecie klikając na poniższe linki

http://www.deszynski.pl/s14/Uznanska/index.html

Jak potężny to wniosek pokażemy to teraz. 

Załóżmy, że chcemy policzyć minimalne zużycie materiału przy budowie układu LC. Wzór na L - indukcyjność cewki znajdziecie tutaj

http://jakpowstajfraktale.blogspot.com/2012/03/prawa-naturalne-fizyka-w-piguce-dla.html

Zakładamy, że mamy ustalony promień r cewki i nie zmieniamy pojemności kondensatora C. Chcemy policzyć maksymalną indukcyjność cewki przy minimalnym zużyciu przewodnika.

Ponieważ pochodna funkcji względem l- długości przewodnika, jest tangensem konta alfa (patrz na rysunek pod pierwszym linkiem), więc maksimum i minimum występuje wtedy gdy, pochodna względem (l), jest równoległa do osi x, wtedy tangens alfa jest równy zero. Przyrównujemy więc pochodną funkcji L(l) do zera, po czym wyliczamy, z otrzymanego wzoru wyliczamy l- długość przewodnika. Należy zwrócić uwagę na to, że otrzymamy kilka rozwiązań, np dla równania kwadratowego otrzymujemy dwa rozwiązania, należy  więc wybrać rozwiązanie przy, którym długość przewodnika jest minimalna.

W przyszłości opiszemy tutaj rozwiązania równań różniczkowych pierwszego i drugiego rzędu.

Nauka powinna być darmowa, nie możemy patrzeć i siedzieć bezczynnie widząc strony z płatnymi rozwiązaniami. Nasz blog jest całkowicie darmowy i tym samym może ukróci ten zbrodniczy proceder.

                            Granice i asymptoty funkcji

                 Twierdzenie de L"Hospitala (Delopitala)

Jeżeli istnieje granica ilorazu pochodnych dwóch funkcji, to istnieje też granica ilorazu tych funkcji i te granice są sobie równe.

Co zapisujemy

Nie możemy nigdzie zdobyć dowodu go twierdzenia więc trzeba potraktować go aksjomatycznie i nauczyć się na pamięć. To bardzo potężne twierdzenie oto parę przykładów:

                     Asymptoty pionowe i ukośne funkcji

 Rozpatrzmy funkcję taką jak pokazano na zdjęciu poniżej

Asymptoty to proste do których zmierza funkcja w nieskończoności. Gdy x zmierza do 2 wtedy wyrażenie w nawiasie zmierza do zera, a tym samym cała funkcja zmierza do nieskończoności. Ponieważ w nawiasie występuje równanie kwadratowe więc cała funkcja zmierza też do nieskończoności dla liczby -2, gdyż kwadrat liczby ujemnej daje liczbę dodatnią. May więc tym samym określone dwie proste, stanowiące asymptoty pionowe dla powyższej funkcji. A dzielenie liczby przez  liczbę bliską zeru to to samo co pomnożyć pierwszą liczbę przez odwrotność tej drugiej małej. Liczba bliska zeru jes przecież ułamkiem. Jeszcze raz powturzymy aksjomat. Podzielić ułamek przez ułamek to to samo co pomnożyć pierwszy ułamek przez odwrotność drugiego. Więcej znajdziecie tutaj

http://jakpowstajfraktale.blogspot.com/2012/05/prawa-aksjomatyczne-logarytmow-dziaania.html

                                   Asymptoty ukośne

Te wyznaczamy z twierdzenia, którego trzeba nauczyć się na pamięć. Oto to twierdzenie:

Asymptota ukośna lewo i prawo stronna, jest to prosta o równaniu

Gdzie (m) oraz (k) wyznaczamy z równań:

Przy czym wyznaczamy dwa rozje (k) badając osobno granice dla plus i minus nieskończoności.

Dalej badamy powyższą funkcję

Tu nie było konieczne zastosowane twierdzenia Delopitala, jednak

bardzo często korzysta się z niego przy wyznaczaniu asymptot.

Mają (m) podstawiamy je do drugiego wzoru

Pamiętamy, że funkcja zmierza do każdej z trzech wyznaczonych asymptot. Nanosząc je  na wykres  logicznie kombinując do logicznej całości, otrzymamy następujący wykres tej funkcji

Zawsze badamy funkcje w jej szczególnych punktach, tutaj są to +2 i -2 z prawej i z lewej strony z osobna dla każdej z tych liczb i pamiętamy, że asymptoty funkcji to proste do , których ta funkcja zmierza w nieskończoności.

Wykresy funkcji można rysować jeszcze dokładniej. Sposób ten opiszemy poniżej.

                       Przebieg zmienności funkcji

Pamiętamy, że miejsca zerowe pierwszej pochodnej podstawione do funkcji wyjściowej (pierwotnej) dają maksima i minima tej funkcji, a miejsca zerowe drugiej pochodnej dają punkty przegięcia funkcji pierwotnej.. W powyższym przykładzie druga pochodna nie ma miejsc zerowych. Punkt przegięcia funkcji to punkt w którym funkcja zmieni swoją krzywiznę z + na -. .

Cdn.

Równania różniczkowe zerowego rzędu

 Ugięcie belki nieobciążonej 

Nie uwzględnimy tu momentu siły działającej na pręt, zrobimy to później. Czynimy to po to by mógł poćwiczyć rozwiązywanie równań różniczkowych zerowego rzędu.

Rozpatrzmy belkę zamocowaną do ściany, tak jak pokazano niżej. Policzymy długość L tej belki po odkształceniu. Beka nie jest obciążona ciężarem więc ugina się skutkiem swojej własnej masy.

Układamy warunek równowagi sił.

Gdy mamy ustalone wychylenie, wtedy siłę grawitacji f równoważy siła sprężystości f =k*s

Zmieniając teraz długość pręta zmienia się też siła f , zmienia się zarówno masa jak i przyśpieszenie.

Takie rozpisywanie bardzo małych zmian, to podstawa działań matematycznych.

Po całkowaniu i różniczkowaniu takich wzorów wychodzą makro wzory.

Stałe c1 i c2  wyznaczymy z warunków początkowych, kiedy t = 0

wtedy wychylenie równe zero i c1 = c2 =Lo

w rzeczywistości koniec pręta będzie opadał ruchem jednostajnie opóźnionym, skutkiem oporu sprężystości materiału. Jednak dla większości przypadków można to zaniedbać.

W artykule

www.latwa-matematyka.blogspot.com

Wyprowadziliśmy wzór dla spadku swobodnego z oporem ośrodka. Kto dociekliwy może sobie tą wielkość podstawić za wychylenie.

Czas t ruchu końca pręta w polu grawitacyjnym wynosi

                                    Prawo Hoke"a

Jest to wzór opisujący naprężenie w pręcie (belce) nieobciążonej.

                              Belka obciążona masą

Znowu układamy równanie sił

Siła pochodząca od nieobciążonego pręta plus siła pochodząca od zawieszonej na jego końcu masy, równa się sile sprężystości.

N - jest momentem siły, równym N = PxR należy ją uwzględnić chcąc dokładnie opisać to zjawisko. Czytelnik już pewnie zauważył, że podany wyżej wzór na długość łuku L jest mocno przybliżony, gdyż nie uwzględnia momentu siły, która przecież istnieje nawet gdy pręt nie jest dodatkowo obciążony. Wyprowadziliśmy taki wzór po to by stopniować stopień trudności. Każdy czytelnik zauważy, że czeka go trudny orzech do zgryzienia.

P- jest siłą pochodzącą od zawieszonej masy równą M*g.

Po prwej stronie równania powinien być minus. R jest x równym L = l*R*cos(alfa), gdzie l jest długością pręta, ściślej długością łuku a L tak jak pokazano na pierwszym zdjęciu bezpośrednią prostą odległością do zawieszonej masy.

Przyrównaliśmy do zera by otrzymać równanie różniczkowe jednorodne, które jest też rozwiązaniem tego równania. Równanie różniczkowe niejednorodne to równanie bez ej operacji. Suma tych dwóch rozwiązań daje też rozwiązanie tego równania różniczkowego. Skoro rozwiązanie szczególne jest rozwiązaniem tego równania więc Stałą c wyznaczymy z warunków brzegowych, które tu ciężko zastosować zastosujemy więc analizę wymiarową, skoro y jest odwrotnością masy więc i stała c musi być jej odwrotnością gdyż sama funkcja wykładnicza jak też logarytmiczna nie posiada wymiaru. Możemy wiec napisać

Bardzo ważny sposób całkowania. Podamy przykład

 To nasz sposób, który zastosowaliśmy w dalszej części tego artykułu. Niestety nie jesteśmy go pewni!!!!!!!!!!!!!!!!!!!!.

Podstawiamy to do równania , ale niejednorodego, możemy tak uczynić gdyż zgodnie z teorią rachunku różniczkowego rozwiązanie szczególne jest rozwiązaniem równania ogólnego. Oznacza to, że poszczególne rozwiązania są tożsame, czyli można je przyrównać do siebie.

Po rozwiązaniu względem d^2(L)/d(t)^2 otrzymamy

Należy zapamiętać to równanie a ściślej to zdjęci, gdyż głowa to nie śmietnik i uczymy się tylko sposobów wyprowadzeń i wniosków końcowych z tych wyprowadzeń.

Pójdziemy teraz równoległą drogą by wyznaczyć d(N). W tym celu robimy rysunek elementarny ugiętej belki, jak by powiększenie jej bardzo małego elementu, czynimy to po to by ułożyć mikro równania, z których przez całkowanie otrzymamy makro równania.

Zastosujemy tu słynne prawo Hoey"a oraz zauważymy, że bardzo mały element powierzchni d(S) = b*d(y)

b - jest wymiarem poprzecznym wymiarem belki i nie ulega zmianie podczas zginania. Oczywiście zmiany te zachodzą, ale są tak małe, że możemy je pominąć.

d(y) - elementarnym wydłużeniem całej długości pręta. Zmiana ta jest bardzo silna, długość prostej belki (przed ugięciem)jest dużo mniejsza od jej wymiarów liniowych, po ugięciu.

Prawo Hoke"a mówi, że prostopadły nacisk siły F na powierzchnię S, równa się

Prawo Hoke"a przedstawia pierwsze równanie na zdjęciu.

Dalsze wyprowadzenie jest zbyt ciężkie by je tutaj zamieszczać, a prace nad nim trwają tutaj

http://jakpowstajfraktale.blogspot.com/2012/07/ugiecie-belki-prawo-hokea-ugiecie-bela.html

.

   Równanie różniczkowe pierwszego rzędu

Równanie różniczkowe pierwszego rzędu wygląda następująco

Z tak określonego równania należy wyliczyć (y). Jest to rozwiązanie wyżej pokazanego równania różniczkowego. Pokazano je na poniższym zdjęciu

Wyprowadzenie rozwiązania - Dowód logiczny

Po pierwsze rozdzielamy zmienne, czyli y-ki przenosimy na jedną stronę a x - sy na drugą.

Po drugie, korzystamy z wcześniej udowodnionego twierdzenia, że całkowanie jest odwrotnością różniczkowania, kliknij na poniższy link, tu umieściliśmy dowód

http://jakpowstajfraktale.blogspot.com/2012/02/00000r0a0chunek-cako0wy-dla-tych-ktorzy.html 

Należy szczególną uwagę zwrócić na fakt iż P(x) jest równe całce(p(x)dx

                                                                  Przykład zastosowania

Rzut poziomy z uwzględnieniem oporu powietrza

Jako przykład weźmiemy ruch poziomy z oporem powietrza. Na początku ciało ma prędkość v0. Skutkiem oporu powietrza prędkość ciała będzie spadać. Siła oporu jest proporcjonalna do prędkości ciała, i równa

                                                                          Fop = k*v

Więcej na ten temat znajdziecie tutaj

http://fizyka-w-pigulce.blogspot.com/

Skutkiem występowania siły oporu ciało będzie zwalniać wytracając prędość. ponieważ następuje zmiana prędkości ciała więc doznaje ono przyśpieszenia, równego (a). ponieważ ma masę więc z drugiego prawa Newtona wiemy, że doznaje ono siły, równej

                                                                         F = m*a

Z fizyki wiemy, że zmiana drogi w czasie równa jest prędkości, a zmiana prędkości w czasie równa jest przyśpieszeniu. Dodając do tych wzorów granicę, gdy czas zmierza do zera, w sposób opisany wyżej, dowiemy się, że prędkość jest pochodną drogi po czasie, a przyśpieszenie jest pochodną prędkości po czasie

Do celów zadania przyjmiemy m*dv/dt = -k*v Po to by otrzymać równanie różniczkowe takie jak przedstawiliśmy wyżej. Znak minus bierze się z faktu, że siła oporu jest przeciwnie skierowana do siły ciągu.

Korzystając z tego, że całkowanie jest odwrotnością różniczkowania więc całkując otrzymaną prędkość po czasie otrzymamy drogę. Więcej na ten temat znajdziecie tutaj

http://jakpowstajfraktale.blogspot.com/2012/02/00000r0a0chunek-cako0wy-dla-tych-ktorzy.html

Całki liczy się ciężko dlatego radzimy skorzystać z serwera liczącego całki. Serwer znajdziecie pod tym adresem

http://integrals.wolfram.com/index.jsp

Który zwrócił nan następującą całkę będącą wzorem na drogę z uwzględnieniem oporu powietrza. Na tym serwerze stałą -k/m wpisujemy jako np. A a za t wstawiamy x, puźniej dokonujemy podstawienia.

                                                

                                                Przykład z siłą wyporu samolotu

Równanie na siłę wyporu samolotu wyprowadza się z równania Bernouliego. Informację na ten temat znajdziecie tutaj

http://fizyka-w-pigulce.blogspot.com/

Ponieważ siła wyporu siła nośna samolotu zależy od gęstości powietrza więc w końcu przy pewnej wysokości zrównoważy ją siła grawitacji., SIŁĘ OPORU POMINIEMY, TYM SAMYM ROZPATRUJEMY LOT SAMOLOTU  BEZ OPORU OTACZAJĄCEGO GO OŚRODKA, ZROBIMY TAK PO TO BY UPROŚCIĆ TO ZADANIE Tto zadanie już jest trudne dla początkujących, również i poniższy przykład. Napiszemy tylko równanie dla takiej sytuacji. Cała sztuka polega na ułożeniu równania równowagi sił po czym twożymy z tego równania równwnie różniczkowe w sposób podany wyżej.

Wypadkowa siła wznoszenia jest równa sile grawitacji minus siła wyporu co zapisujemy

                               m*a = -m*g - C*S*q(h)*v2/2

W sytuacji już ustalonej wysokości siła ciągu skierowanego do góry zanika, zrównoważona przez siłe grawitacji tak, że pozostaje rozwiązać równanie

                               m*g  = - C*S*q(h)*v2/2

g- przyśpieszenie ziemskie

c - stała bezwymiarowa siły wyporu zależna od kształtu skrzydeł samolotu, dużo mniejszym stopniu zależna od kształtu kadłuba

S - powierzchnia skrzydeł

q - gęstość powietrza zależna od wysokości

v - prędkość liniowa samolotu

m*g traktujemy jako stałą gdyż zmiana przyśpieszenia ziemskiego g, w przypadku samolotu można zaniedbać, jednak w przypadku lotów kosmicznych trzeba założyć zmienne g.

 Dalej w formie zdjęć

Ponieważ q zależy od wysokości, która pośrednio zależy od czasu t, więc za d(t) podstawiamy d(h). Wzór na q(h) znaleźliśmy w internecie. Stałą zaś wyciągamy przed całkę. Dodamy jeszcze, że 

                                     całka(1)*d(x) = x

(Stała całkowa c, którą pominęliśmy na tym razem poniższym zdjęciu, jest równa v0. W ogóle stałe całkowe wyznaczamy z warunków początkowych danego zjawiska, lub końcowych.) 

Najczęściej jedynki nie piszemy wtedy mamy

                                          całka d(x) = 1

Niefortunnie występują w powyższym wzorze dwa oznaczenia c, należy pamiętać, że pierwsza stała c na zdjęciu to stała wyporu

q0 -  gęstość przy gruncie

R -  stała Rytberga

M -  masa molowa powietrza lub innego ośrodka

T - temperatura ośrodka

W ten sposób otrzymujemy wzór na prędkość wznoszenia samolotu

                                                                                                                                                                                                                                                                                                                                                                                                                                         

h(t)  = 1/2*a*t^2

Gdyż samolot posiada wypadkowe przyśpieszenie skierowane do góry. Możemy siłę grawitaci i opór pominąć gdyż takie są powyższe założenia Niżej, przy rozwiązywaniu równania różniczkowego nie jednorodnego, wyprowadzono wzór na prędkość z uwzględnieniem oporu powietrza i siły grawitacji. Pochodna tej prędkości po czasie da przyśpieszenie (a). Da to jeszcze lepsze przybliżenie otrzymanego niżej wzoru na wysokość lotu samolotu.Podstawiając te wzory do równania , wyprowadzonego tutaj na h(t) otrzymamy równania z uwzględnieniem siły grawitacji i oporu. Kto ma ochotę, może podstawić to do wzoru przedstawionego na drugim poniższym zdjęciu zdjęciu (To będzie żmudna robota).

Całki powyższego równania serwer nie potrafi policzyć. By policzyć drogę konieczna jest znajomość równań różniczkowych drugiego rzędu. Można jednak w przybliżeniu policzyć tą drogę całkując p(x) nie po czasie lecz po wysokości h, na pierwszym zdjęciu, gdzie jest klamrą zaznaczony układ równań, pomijamy ostatnie równanie, które uwzględnimy dopiero po wyliczeniu drogi h(t). Żeby serwer policzył nam taką całkę trzeba pozbyć się plusa, po przez zastosowanie przybliżenia, które pokazujemy na poniższym zdjęciu, przy czym bierzemy do równania pierwszy wyraz rozwinięcia, następnie naprawiamy równanie analizą wymiarową.

W ten sposób otrzymaliśmy przybliżony wzór na wysokość lotu samolotu

Funkcja erf , silnie zmierza do zera dla t zawartego od 1 do 3 sekund. powoduje to bardzo silną siłę przyziemiającą od chwili uzyskania prędkości nośnej v0 i twa około przez trzy sekundy początkowego lotu. Po upływie tego czasu bardzo silnie zmierza do jedności.

Teraz rozumiemy powiedzenie, że najniebezpieczniejsza jest faza startu i lądowania. Wzór wydaje nam się być dość dokładny po mimo to, że pominęliśmy siłę przyciągania ziemskiego m*g oraz siłę oporu. Naszym zdaniem napewno ten wzór pokazuje sedno problemów z jakimi mierzy się przemysł lotniczy. Można ten wzór dodatkowo uściślić. Zauważmy, że różniczując po czasie otrzymany wyżej wzór na pdkość wznoszenia samolotu, otrzymamy jego przyśpieszenie, jednak jest to przyśpieszenie bez uwzględnia siły grawitacjii, czyli tym samym taki wzór opisuje stan nieważkości. 

Należy jeszcze odjąć drogę wynikającą z siły oporu, co pokazaliśmy na powyższym zdjęciu. W tym przypadku

                                   h(t) = vop*t

My tego równania nie pokarzemy, gdyż rozmiar zeszytu stał się za mały. Jeszcze  raz przypominamy, za v należy podstawić po niżej wyliczone v.

Niech karzdy czytelnik sam się zastanowi czy należy odejmować drogę 1/2*g*t^2. My sami nie jesteśmy pewni. Droga vop*t zawiera już w sobie tą drogę, widać to w poniżej ułożonej równowadze sił. Możliwe że sama ta droga wystarczy. Zauważmy jak pięknie zgrało się powyższe przybliżenie lotu, stosując niżej wyprowadzone wzory otrzymujemy rozwiązania z oporem powietrza. Te równania stanowią całość kompletny układ równań dla ciała którego gęstość jest dużo większa od gęstości otaczającego go powietrza. Niestety tych równań nie da się zastosować do opisu np. napompowanego balona gdyż w takim przypadku dużą rolę odgrywa siła wyporu statycznego, której w tych równaniach nie uwzględniliśmy.

Stanowi to końcowe rozwiązanie

Równanie różniczkowe pierwszego rzędu nie jednorodne

Jest to równanie, w którym stała C występująca w rozwiązaniu powyższego równania, jest zmienną zależną od x. Wtedy rozwiązanie takiego równania wygląda następująco. Dodamy tylko że 

                                                                     y = c*e^P(x)

W ten sposób poniższe równanie jest powiązane z powyższym.

Przykład. Rzut pionowy z uwzględnieniem oporu powietrza

Na ciało rzucone do góry działają siły Grawitacji i oporu powietrza. Wypadkowa siła to

                                                       m*a = -m*g - k*v

Gdzie m*a jest siłą wypadkową. Następnie przyśpieszenie a przedstawiamy w postaci 

                                                               a = d(v)/d(t)

Siła m*g przyjmujemy jako stałą gdyż rozpatrujemy niewielką wysokość rzutu. Pierwsze równanie przedstawimy w postaci

                            m*d(v)/d(t) + k*v= -m*g 

Po podzieleniu obu stron równania przez m otrzymamy równanie różniczkowe nie jednorodne

                                 d(v)/d(t) + k/m*v= -g 

Łatwo udowodnić przeprowadzając ponownie przedstawiony wyżej dowód, że 

                                                             U(t) = -g 

i jest stały

A                                                            P(t) = k/m

                Całka P(t)*d(t) = k/m*całka(d(t)) = k/m*t

Po podstawieniu tych równań do wzoru na rozwiązanie równania różniczkowego niejednorodnego otrzymamy

Zamoiast S0 powinno być V0

Dodamy tylko, że całka sumy wyrazów lub różnicy jest równa sumie całek!!!!!!!!!!!!!!

      Rzut ukośny z oporem powietrza. Krzywa balistyczna

Poprzednio otrzymaliśmy wzór na drogę w rzucie poziomym. W rzucie ukośnym wypadkowa prędkość rozkłada się na prędkość w kierunku x i h - który jest wysokością. Prędkość w kierunku x

                                     v(x) = vw*cos(alfa)

A w kierunku h 

                                     v(h) = vw*sin(alfa)

Tak więc otrzymane drogi wystarczy pomnożyć przez sin i cos

Zamiast S0 powinno być V0

Ostatni przykład kończący ciąg trudności. Dodamy tu analizę wymiarową. Dalej wyjaśnimy czym ona jest.

   Ruch drgający ciała zawieszonego na sprężynie - Wahadło

Tak jak poprzednio układamy równanie sił

Wypadkowe przyśpieszenie

                                        m*a

będzie równe sile sprężystości

                                          k*x

której kierunek jest okresowy raz jest zgodna raz przeciwna, to samo tyczy się siły m*a, która działa raz zgodnie tym razem z siłą grawitacji m*g , raz przeciwnie.

Jednak jak pokazujemy na zdjęciu gdy za przyśpieszenie podstawimy drugą pochodną po czasie wtedy otrzymamy równanie różniczkowe drugiego rzędu, o którym będziemy pisać w tym blogu w przyszłości. Dlatego sprowadzamy to równanie do równania różniczkowego pierwszego rzędu, wykorzystując pierwsze równanie pokazane na zdjęciu.

Kto nie rozumie pierwszego równania powinien zapoznać się z całym artykułem, który znajdzie klikając na poniższy link

http://jakpowstajfraktale.blogspot.com/2012/03/prawa-naturalne-fizyka-w-piguce-dla.html

Periodyczność wychylenia za gwarantujemy mnożąc x przez cos(alfa), zmianę konta za gwarantujemy równaniem

                                     afa = omega*T

gdzie

omega = 2*(pi)/T

T - jest okresem drgań, który łatwo można zmierzyć

Tak więc

                                  x(T) = x0*cos(omega*T) 

gdzie x0 - jest początkowym wychyleniem, które my nadaliśmy rozciągając sprężynę 

Prędkość drgań osiągniemy różniczkując powyższe równanie względem okresu T. Dalej w formie zdjęć

Przy czym wypadkowa siła jest zawsze przeciwnie skierowana do siły sprężystości, dlatego dajemy przeciwny znak

Całka prędkości po czasie da wychylenie x(T).

Jest to droga ciała bez siły tłumiącej. Siła grawitacji nie jest siłą tłumiącą .

Jest to wzór przybliżony, gdyż nie uwzględniliśmy sinusa z tego powodu, że całka byłaby zbyt skomplikowana do policzenia.

Równanie różniczkowe drugiego rzędu i n-tego rzędu. Ogólne rozwiązanie równań różniczkowych n-teg rzędu o współczynnikach stałych.

Ogólnym rozwiązaniem tego typu  równań różniczkowych jest funkcja

Trzeba sobie przypomnieć dział matematyki dzielenie wielomianu przez wielomian, gdyż r występuje w takiej potędze, jak rząd równania różniczkowego. Dla równania różniczkowego trzeciego rzędu r będzie w trzeciej potędze co oznacza trzy rozwiązania. Tą uniwersalność zawdzięczamy własności funkcji potęgowej y = e^(r*x), a ściślej jej pochodnej, której wzór wygląda następująco. Stałe q i P nie można uzmienniać, tym samym oznaczają dowolne stałe nie zależne od x.

     Dowód dla równania różniczkowego drugiego rzędu

a

Można by bardzo łatwo sprawdzić czy wzór powyższy zachodzi dla uzmiennionych stałych, ale każdy czytelnik zrobi to we własnym zakresie.

Twierdzenie

Suma poszczególnych rozwiązań równania różniczkowego jest też rozwiązaniem tego równania.

Dalszy dowód leży w zakresie czytelnika. Jest łatwy wystarczy podstawić rozwiązanie do równania różniczkowego, różniczkujemy je dwó i jednokrotnie. Jeżeli rozwiązanie jest poprawne powinniśmy otrzymać - lewa strona równa prawej – stronie równania.

Rozwiązanie równania różniczkowego- tożsamość różniczkowa

Najpierw udowodnimy wzór na moment pędu L, który z definicji równa się

                                      L = m*v*r

Na zdjęciu pokazaliśmy sposób przejścia do innego zapisu tej wielkości

Zbadamy teraz jak zależy promień wodzący punktu m czyli jego tor ruchu od konta, który zależy od czasu.

Zastosujemy tu pewne przekształcenie matematyczne oto ono

Zauważmy że tak naprawdę kont fi skraca się i otrzymujemy klasyczną definicję prędkości. Równanie na prędkość przedstawiliśmy w takiej postaci gdyż pochodna kąta po czasie równa się omedze, którą wyprowadziliśmy na pierwszym zdjęciu. Możemy więc przedstawić to równanie w postaci:

By lepiej zrozumieć tą konwencję wyciągania pochodnej, podamy przykład

Całkowita pochodna równa się pochodna funkcji zewętrznej, gdzie fi traktujmy jako x razy pochodna funkcji wewnęŧrznej fi, gdzie t tym razem traktujemy jako x.

Ponieważ szukamy przyśpieszenia więc z powyższego równania wyciągamy pochodną, Pamiętając , że r zależy od fi i od czasu, czyli jest funkcją uwikłaną, oraz dalej stosujemy wyżej opisaną sztuczkę.

Jest to dość ciężkie więc wyprowadzeniu pokazanemu na poniższym zdjęciu trzeba poświęcić trochę uwagi.

W ten sposób otrzymaliśmy przyśpieszenie, jednak to jeszcze nie jest koniec. Zwróćmy uwagę na nawias, otóż ktoś zauważył, że druga pochodna z funkcii,  którą oznaczymy

                                       

                                          b = 1/r,

 jest równa wyrażeniu w nawiasie

                                         Dowód

Tu też przykład, w tym przypadku r zależy od fi a fi nie zależy od czasu.

W tym przypadku r traktujemy jako zależne od samego siebie.

Przy czym zachodzi to tylko wtedy gdy b zależy od kąta fi a ten nie zależy od czasu!!!!!!!!!!!!.

To bardzo potężny wniosek

W powyższym wyprowadzeniu r zależy od kąta fi więc jest funkcją złożoną!!!!!.

Więc przyśpieszenie możemy zapisać w postaci:

Przed całym wyrażeniem powinien być minus.

Lub w bardziej przejrzystym zapisie

Bardzo potężne równanie. Jako przykład wyprowadzimy wzór na tor ruchu cząstki w polu sił centralnych.

Układamy równanie sił, wypadkowa siła będzie równa sile grawitacji minus siła odśrodkowa działająca na cząstkę

Za drugą pochodną r podstawiamy wcześniej wyliczony wzór

Zależność promienia od czasu została wyprowadzona tutaj. Kąt fi wprowadziliśmy sztucznie, przez co nie rozpatrujemy w tym przypadku pola sił centralnych. W polach sił centralnych droga nie zależy od kąta.

http://jakpowstajfraktale.blogspot.com/2012/01/tor-ruchu-meteorytow-spadajacych-na.html

Druga całka z cos(fi)^(-1) wygląda następująco

Dwo krotna całka z jedynki da

                                                 C1*(fi)

kąt ten policzymy ze wzoru, który został wyprowadzony tutaj

http://jakpowstajfraktale.blogspot.com/2012/01/uniwersalny-wzor-na-cosinus-i-sinus.html

Prędkość policzymy w następujący sposób

Gdzie za r wstawiamy wcześniej wyliczone r.

Bardzo długi i skomplikowany wzór

Można też rozwiązać to równanie w następujący sposób gdy założymy, że r nie zależy od fi

C1 i C2 trzeba wyznaczyć z warunków brzegowych.

Na koniec najogólniejsza postać tego równania

Zauważymy, że:

Wraz ze wzorami na podany wyżej sinus i kosinus, otrzymujemy bardzo mocną całość prawdzią potęgę

W wyżej wymienionym posście ( jeszcze raz link do niego)

http://jakpowstajfraktale.blogspot.com/2012/01/tor-ruchu-meteorytow-spadajacych-na.html

zależność promienia od konta fi została wprowadzona sztucznie, Tam jest dowód, że w polu sił centralnych prędkość nie zależy od kąta, Ten kąt twoży się skutkiem wyżej opisanego równania.

Jeżeli w tamtym równaniu nie stosować przybliżenia tylko wyciągnąć stałą przed pierwiastek wtedy...........

Ale karzdy czytelnik sam się domyśli o co chodzi.

Oczywiście chodzi na  prędkość gdyż ta występuje w powyższym wzorze, lub wyrażając się ogólnie matematycznie, o pierwszą pochodną funkcji po x-sie

Cdn.

Bardzo przydatne wzory

Są to bardzo ważne wzory, bez nich nie sposób wyobrazić sobie rozwiązywania skomplikowanych równań matematycznych. Choć rozwinięcia w szereg nie dają dokładnych wyników to jednak można wziąć dowolną liczbę sum danego wzoru i otrzymać wynik z dowolną dokładnością.

Pierwszy wzór nie wiemy kto wyprowadził

Drugi wzór to szereg Maclarena, opiera się na sumie pochodnych funkcji. liczba a jest punktem wokół którego rozwijamy funkcję, prawie zawsze jest to zero lub jeden.f(a)" oznacza wartość pochodnej po podstawieniu liczby a za x. Za e^x podstawiamy dowolną funkcję f(x).

Kto wyprowadził trzeci wzór, też nie wiemy.                                   

http://jakpowstajfraktale.blogspot.com/

                                                       Rachunek całkowy

Poniższy wykład został przedstawiony tylko dla funkcji f(x) = a*x, Tym samym wzór na całkę podany niżej, jest poprawny tylko dla tej funkcji, nie mniej jednak oddaje samo sedno całkowania, a oto Nam przecierz chodziło, o to by oddać sedno całki bez wdawanie się w szczegóły, które choć ważne to jednak zaćmiewają ogólny obraz całkowania u osób, które nie chodzą na studia. To samo tyczy się rachunku różniczkowego i tensorowego które znajdziecie po poniższymi adresami

http://jakpowstajfraktale.blogspot.com/2012/02/rachunek-rozniczkowy-wykad.html

http://jakpowstajfraktale.blogspot.com/2012/02/blog-post.html

Tu też nie wdawaliśmy się w zbędne szczegóły. Wykład został przedstawiony w formie zdjęć

 i został zamieszczony pod poniższym adresem

http://jakpowstajfraktale.blogspot.com/2012/02/00000r0a0chunek-cako0wy-dla-tych-ktorzy.html

Wogóle cała nasza strona dedykowana jest przedewszystkim dla takich osób, zamieściliśmy na niej zagadnienia z fizyki i mamtematyki z zastosowaniem metod matematycznych spotykanych na studiach

Do każdej całki należy dodać stałą (C), którą wyznacza się z warunków brzegowych otrzymanej funkcji, np gdy mamy funkcę prędkości do tego wzoru podstawiamy prędkość równą zeru, to co zostanie po takim podstawieniu jest właśnie tą stałą.

Dla bardziej dociekliwych udowodnimy, że całkowanie jest odwrotnością pochodnej.

wykład na temat pochodnej zamieściliśmy tutaj

http://jakpowstajfraktale.blogspot.com/2012/02/rachunek-rozniczkowy-wykad.html

W tym celu równanie

Przekształcimy w następujący sposób

Definicja całki na zdjęciu powyższym bierze się z konieczności by ta pochodna zmierzała do f(xi) gdy delta x zmierza do xi.

Dokładny wzór całki z przedstawionego wyżej ciągu logicznego jest taki jak pokazuje zdjęcie poniższe, jednak jest to nie uznana oficjalnie przez świat naukowy wersja. Oficjalnie uznany wzór pola pod dowoną krzywą pokazuje zdjęcie powyższe

 

Serwer liczący całki

http://integrals.wolfram.com/index.jsp

http://integrals.wolfram.com/index.jsp?expr=n*e%5E%28ln%281%2F2*r*x%5E2%29&random=false

Radzimy korzystać z tego serwera, po co się biedzić i grzebać się w tych małych przyrostach skoro już ktoś to zrobił. Mając równanie chcemy szybko otrzymać wynik

                    Całki podwójne i n-tego stopnia

Przykład pokazaliśmy na zdjęciu. Sprawa jest naprawdę prosta. Ponieważ całkowanie jest odwrotne do różniczkowania więc to samo tyczy się pochodnych.

Całkowanie przez części - Bardzo ważny wzór

Podamy ten wzór bez dowodu. Jeżeli znamy funkcje h(x) taką, że pochodna tej funkcji równa się f(x), wtedy zachodzi wzór

Metoda całkowania przez części wynika ze wzoru

 na pochodną iloczynu funkcji f(x) i g(x)

Bardzo potężnym narzędziem całkowania jest metoda całkowania przez podstawienie

Oto bardzo przydatny wzór

Przykład dla n = -1

Gdyż pochodna cosinusa  równa się minus sinus g(x) = cos(x)

Zwróćmy uwagę jak wielką pracę wykonali matematycy. Musieli szukać takich całek funkcji, których pochodne dają z powrotem funkcję całkowaną. Wiele z tych poszukiwań to odgadnięcia, a sprawdzanie odbywało się po przez podstawienie do wzoru na pochodną funkcji.

Pola powieżchni funkcji

Zaczniemy od wzorów przejścia z układu opisanego przez x i y - (Kartezjańskiego do układu opisanego przez kąt fi i r promień - (układ biegunowy)

                                              Płaszczyzna

Odrazu wykresy przygotowane są do pisania mikro wzorów. Zauważmy, że gdy kąt fi bardzo mały, a taki przypadek rozpatrujemy pisząc mikro wzory, wtedy łuk fi możemy w granicy gdy fi zmierza do zera potraktować jako prostą.

                                            Przestrzeń

Wzory te można udowodnić logicznie z przedstawionego wyżej wykresu, jednak nie jest to prosta sprawa w przypadku przestrzeni, która jest opisana przez dwa kąty. Lepiej zrozumieć je raz i zapamiętać aksjomatycznie.

                                         Pola powierzchni funkcji obrotowych

Drugi sposób liczenia pola tomnożenie funkcji f(x) =y przez jej długość łuku. Pełny kont obrotu wynosi 2*pi, wystarczy więc pomnożyć y*d(L) przez tą liczbę a otrzymamy pole powierzchni obrotowej

W pierwszym równaniu, wielkości pod pierwiastkiem pomnożyliśmy i jednocześnie podzielliliśmy przez delta x kwadrat. Po wyciągnięciu delta x kwadrat przed nawias i po dodaniu limesu gdy delta x zmierza do zera, otrzymujemy końcowy wzór na pole powierzchni obracanego równania okręgu. Oczywiście może to być dowolna funkcja, na zdjęciu przedstawiliśmy równanie okręgu.

Pole powierzchni równe jest

delta(s) = (yi)*delta(L)

Stąd w drugim równaniu na zdjęciu wzięło się yi. Popatrzmy jeszcze raz na zdjęcie, gdy z delta(L) zmierzamy do zera otrzymamy Li w punkcie, a suma tych punktów pomnożona odpowiednio przez yi da nam pole powieżchni. Po dodaniu limesa do tej sumy, dostajemy całkę i końcowy wzór. 2*(pi) jest obrotem i równa się pełnemu obrotowi = 360 stopni. Pi jest liczbą = 3,14

y prim - jest pochodną funkcji y.

Jeżeli pominiemy 2*pi wtedy otrzymamy normalne pole, możemy więc napisać równość

        Wzory na długości krzywych opisanych dowolną funkcją

Jeżeli mamy teraz funkcje x i y zależne od b, gdzie b może np. oznaczać czas, wtedy dzieląc i mnożąc wielkości pod pierwastkiem przez delta(b) do kwadratu, oraz wyciągając (delta(b))^2 przed pierwastek, otrzymamy dwa wzory na długości L:

pierwszy podany wyżej i drugi zadany przez zmienną b.

To są długości krzywych jedno i dwówymiarowe. Dodając kolejne sumy w wyrzej opisany sposób otrzymamy długości krzywych w n -wymiarach. To bardzowarzne ogólne wzory, podstawy. Z nich wyskakują wzory dla poszczególnych przypadków.

Przykład

Długość krzywej dwówymiarowej w układzie biegunowym

http://jakpowstajfraktale.blogspot.com/

          Całka powierzchniowa nie uwzględniająca obrotów

Jeżeli w układzie biegunowym dana jest funkcja f(r) i porusza się ten promień po kącie fi, wtedy pole zakreślone przez ten promień wodzący wyraża się wzorem

gdzie r = f(r). Tak, że w tym przypadku możemy przyrównać poprzednie sposoby obliczania pól do tego sposobu.

                                                       Dowód

Elementarna powierzchnia o bokach a = r*d(fi) i b = d(r) ma powierzchnię

Przykład

Ja Skorzystałem z serwera liczącego całki.

http://www.wykop.pl/ramka/117341/serwer-obliczajacy-calki-nieoznaczone/

Jeżeli pole powierzchni przedstawione powyższym wzorem obrócimy wokół własnej osi wtedy otrzymamy wzór na pole powierzchni figur obrotowych.

                                   Pole płata na sferze

Patrzymy na rysunek i układamy mikro równanie

Powyższy wzór wyprowadziliśmy błędnie. Oto poprawne rozwiązanie
Pole płata - układ kartezjański

Zauważymy, że Modół tego pola N jest równy
N = (Zx^2+Zy^2+1)^(0,5)
a delta s = N*delta(G)
gdzie delta(G) = d(x)*d(y) i jest elementarną powierzchnią. Jedynka we wzorze występuje dlatego, gdyż w kierunku Zx mamy wersor jednostkowy, liczymy pole nie objętość.
Iloczyn tego modułu N razy delta (G) = delta(S), a całka podwójna po d(x) i d(y) da pole powierzchni.

                          Pole powierzchni figur obrotowych

Jest to uogólniony wzór na powyższe pole, zmienna nie koniecznie musi być kątem fi.

                                                Przykład

Obliczyć objętość torusa.

Przykład

Obliczyć objętość ostrosłupa, którego tworzącą jest linia prosta f(x).

Innym sposobem liczenia objętości jest całka podwójna , w której wykorzystuje się elementarne pole d(G), wyprowadzone na samym początku. 

Zakładamy tutaj, że f(r) = f(x,y).

Przykład obliczyć objętość między dwoma okręgami danymi równaniami tak jak na poniższym zdjęciu.

Szukana objętość jest różnicą objętości większej danej pierwszym równaniem i objętości mniejszej.

Liczymy objętość pierwszą, oznaczymy ją A

Powinno być

Trzeci układ to układ cylindryczny. wzory przjścia z x na r i fi wyglądają następująco.

Całka potrójna w układzie cylindrycznym.

 Układamy wzór na mikro objętość, który po scałkowaniu da nam makro objętość

Nie będę udawał, że wiem skąd wzięła się we wzorze 1/3. Prawdopodobnie stąd, iż r jest też w pośredni sposób zależne od z. 2/3 wprowadziliśmy skutkiem rozwiązana równania, które pokazuję niżej.

Przykład

Liczyliśmy objętość kuli, a ta w każdym układzie powinna wynosić

                                         V = 4/3*pi*R^3

Stąd pojawiła się konieczność wstawienia do wzoru 2/3. Tym samym trzeba na ten wzór uważać, gdyż nie został wyprowadzony logicznym ciągiem. fi oczywiście zmienia się od zera do pi. Przepraszam za błąd.

 Całka potrójna objętościowa w układzie sferycznym

Znów układamy mikro równanie. Na rysunku składowe elementarnej objętości zostały pokazane.

Gdy scałkujemy po d(R) otrzymamy1 /3*R^3 za który jak to poprzednio robiliśmy wstawiamy dowolną funkcję f(R) zależną od teta i fi.

Do każdej całki powinienem doda stałą C. Przepraszam za tak poważny błąd, jednak dopiero teraz to zrozumiałem i nie chce mi się od nowa poprawiać prawie wszystkich zdjęć. Do każdej całki koniecznie należy dodawać stałe, bez tego, gdy warunki początkowe nie są zerowe, pominięcie tej stałej powoduje błędny wzór!!!!!!!!!!!!!!!!!!!!.

Ani w jednym ani w drugim wzorze niepowinno się całkować po d(r), przed podstawieniem funkcji f(r). Idąc od samej góry powinno być

CDN.

                                                       Rachunek Tensorowy

Rachunek Tensorowy

Wykład przedstawiliśmy w formie zdjęć, najlepiej skopiować te zdjęcia do komputera gdzie można je dowolnie powiększyć. Nie wdawaliśmy się tutaj w szczegóły rachunku tensorowego, chodzi nam o pokazanie samego sedna takiego rachunku. Ogólnie mówiąc tensor to tablica o równej ilości kolumn i wierszy, gdzie są specjalne wzory, które pozwalają wyliczyć taką tablicę. Nie wyprowadzaliśmy tego wzoru jest on podany bez dowodu matematycznego, więc po prostu trzeba go zapamiętać. Nie jest bardzo skomplikowany i przedstawiony jest na zdjęciu poniżej.

Tensorem nazywamy macierz (Tablicę) kwadratową o w-wierszach i k-kolumnach. Rozwiązanie tej tablicy , inaczej zwane Jakobianem przejścia, podaje wzór na ponższym zdjęciu. Przez det rozumiemy macież powstałą po skreśleniu ktej kolumny i wutego wiersza, tak jak na poniższym rysunku.

Przy czym konwencja obliczeń jest prosta, mianowicie ustalamy kolumnę i na tej kolumnie skreślami wiersze. We zorze zmieniamy kolejno numery (w) od 1 do (k )

Zostawimy wynik w te postaci, gdyż dojdziemy do bardzo ważnego wniosku. Otóż gdy mamy tensor symetryczny, to znaczy taki w którym wyrazy mieszane są sobie równe lub są równw zeru, a21=a12 wtedy rozwiązaniem takiego tensora jest iloczyn wyrazów występujących na przekątnej tensora. W znakomitej większości zagadnień fizycznych mamy niezerowe wyrazy na diagonali pozostałe składowe macierzy są tak małe, że można je pominąć. Gdy nie są małe wtedy stosujemy wzur pokazany na zdjęciu pierwszym.

Oto cała tajemnica rachunku tensorowego

Można też wstawiać różniczki oznaczające bardzo małe przyrosty w danych kierunkach

Do tensora wstawiamy dowolne liczby i funkcje tak by osiągnąć zamierzony cel. W zagadnieniu trzech ciał tablica przestaje być symetryczna.

Mamy nadzieję, że udało Nam sięwytłumaczuć tachunek tensorowy w zrozumiały spsób. 
Można się wspomódz stroną podaną niżej, jest świetna.

http://pl.wikibooks.org/wiki/Metody_matematyczne_fizyki/Metody_matematyczne_fizyki

Życzymy dobrej zabawy.

To prawdopodobnie kończy nasz kurs matematyki połączonej z fizyką, dla Was.

Jednak zdecydowaliśmy się kontynuować. To nasz ostatni wpis w tym blogu. Natrafiliśmy na coś co bardzo ułatwi wam życie.

Równanie różniczkowe drugiego rzędu i n-tego rzędu. Ogólne rozwiązanie równań różniczkowych n-teg rzędu o współczynnikach stałych.

Ogólnym rozwiązaniem tego typu  równań różniczkowych jest funkcja

Trzeba sobie przypomnieć dział matematyki dzielenie wielomianu przez wielomian, gdyż r występuje w takiej potędze, jak rząd równania różniczkowego. Dla równania różniczkowego trzeciego rzędu r będzie w trzeciej potędze co oznacza trzy rozwiązania. Tą uniwersalność zawdzięczamy własności funkcji potęgowej y = e^(r*x), a ściślej jej pochodnej, której wzór wygląda następująco. Stałe q i P nie można uzmienniać, tym samym oznaczają dowolne stałe nie zależne od x.

     Dowód dla równania różniczkowego drugiego rzędu

a

Można by bardzo łatwo sprawdzić czy wzór powyższy zachodzi dla uzmiennionych stałych, ale każdy czytelnik zrobi to we własnym zakresie.

Twierdzenie

Suma poszczególnych rozwiązań równania różniczkowego jest też rozwiązaniem tego równania.

Dalszy dowód leży w zakresie czytelnika. Jest łatwy wystarczy podstawić rozwiązanie do równania różniczkowego, różniczkujemy je dwó i jednokrotnie. Jeżeli rozwiązanie jest poprawne powinniśmy otrzymać - lewa strona równa prawej – stronie równania.

Cdn.

Bardzo przydatne wzory

Są to bardzo ważne wzory, bez nich nie sposób wyobrazić sobie rozwiązywania skomplikowanych równań matematycznych. Choć rozwinięcia w szereg nie dają dokładnych wyników to jednak można wziąć dowolną liczbę sum danego wzoru i otrzymać wynik z dowolną dokładnością.

Pierwszy wzór nie wiemy kto wyprowadził

Drugi wzór to szereg Maclarena, opiera się na sumie pochodnych funkcji. liczba a jest punktem wokół którego rozwijamy funkcję, prawie zawsze jest to zero lub jeden.f(a)" oznacza wartość pochodnej po podstawieniu liczby a za x. Za e^x podstawiamy dowolną funkcję f(x).

Kto wyprowadził trzeci wzór, też nie wiemy.                                   

Równania filis - kołowe zamknięte

Wychodząc z definicji pochodnej, (została opisana w posście (Tor Ruchu Meteorytów Spadających Na Słońce) otrzymujemy dla dowolnej funkcji wielkość, którą nazwaliśmy Delta Alfa

Przy wyprowadzeniu tej wielkości posłużymy się trójmianem kwadratowym.

d(f(x))/d(x)=(2*a*x*(delta.x)+a*(delta.x)^2+b*(delta.x))/d(delta.x)

z rysunku widać, że

delta.x=(x2)-(x1)=d=d(f(x))/(d(x)*dx)

Zauważmy, że w przybliżeniu

(delta.x)^2=(delta.x)^2=(d(f(x))/(d(x)*d(x)))^2

i

2*a*x*d(f(x))/(d(x)*d(x))=d(f(x))/d(x)*d(f(x))/(d(x)*d(x)

oraz

b*(delta.x)=(d(f(x)/d(x))/(d(f(x))/(d(x)*dx))

Stąd

(delta.alfa)=(((d(f(x))/(d(x)*d(x))*d(f(x))/(d(x)*d(x)))+(d(f(x))/(d(x)*d(x)))^2+((d(f(x)/d(x))/(d(f(x))/(d(x)*dx)))/((d(f(x))/d(x)))

To był osobny temat

Teraz wyliczamy sinus i kosinus, w tym celu znów korzystamy z definicji pochodnej dla funkcji kwadratowej podanej wyżej.

d(f(x))/d(x)=(2*a*x*(delta.x)+a*(delta.x)^2+b*(delta.x))/d(delta.x)

Zauważmy, iż w liczniku mamy składowe wektora z (w1) i (w2)), wektor W3 =(delta.x)^2 pominiemy jako bardzo mały.

(W2)^2=(2*a*x*(delta.x))^2=4*a^2*x^2*(delta.x)=(f(x)*(d(f(x))/(d(x)*d(x)))^2

(W2)=d(f(x))/d(x)*d(f(x))/(d(x)*d(x)

(W1)^2=(a*(delta.x)^2)^2=(d(f(x))/(d(x)*d(x))^2)^2

(W1)=(d(f(x))/(d(x)*d(x))^2

Znów korzystamy ze słynnego równania Pitagorasa (często pojawia się w naszych postach).

(Ww)=((W1)^2+(W2)^2)^(1/2)=(f(x)*(d(f(x))/d(x))^2+(d(f(x))/(d(x)*d(x))*d(f(x))/d(x))*((d(f(x))/d(x)))^2)^2)(1/2)

sin.u(alfa)=(W1)/(Ww)=(d(f(x))/d(x)*d(f(x))/(d(x)d(x))/((d(f(x))/(d(x)d(x))^2)^2+(d(f(x))/(d(x)d(x))^2)^2)^(1/2)
cos.u(alfa)=(W2)/(Ww)=(d(f(x))/(d(x)d(x)))/((d(f(x))/(d(x)d(x))^2)^2+((df(x)/dx)^2*(d(f(x))/(d(x)d(x)))^2)^(1/2)

(delta.alfa)=(((d(f(x))/(d(x))*d(f(x))/(d(x)d(x)))+((d(f(x))/(d(x)*d(x))/((d(f(x))/(d(x)dx))
Oto trzy bardzo ważne dla nas równania

Nie jest to zwykły sinus i kosinus, lecz uniwersalny zawierające w sobie sinus i kosinus zwykły.
Stałą b pomijamy gdyż przesówa tylko ona delta.x

(W2)^2=(2*a*x*(delta.x))^2=4*a^2*x^2*(delta.x)=(f(x)*(d(f(x))/(d(x)*d(x)))^2
(W2)=d(f(x))/d(x)*d(f(x))/(d(x)*d(x)
(W1)^2=(a*(delta.x)^2)^2=(d(f(x))/(d(x)*d(x))^2)^2
(W1)=(d(f(x))/(d(x)*d(x))^2

Dzieląc sinus przez kosinus otrzymujemy

tg(alfa)=d(f(x))/d(x)

Co należało udowodnić

Weźmy dla przykładu wzór pracy

                                                                     W = F*S*cos(alfa)

Ponieważ działa sił więc mamy do czynienia z ruchem jednostajnie przyśpieszonym

                                                                      S(t) = 0,5*a*t^2

przyśpieszenie i siła są stałe więc naszą fynkcją jest f(x)=S(t)

wyliczając  pochodną i wstawiając do wzoru na cosinus otrzymamy równanie omegę to znaczy zamknięte, zawierające w sobie wszystkie możliwe kosinusy, czyli równanie w przestrzeni możliwości.

Jest to przestrzeń możliwych prac

                 W = F*S*[SUMMA(i=0 ; 00 )(1/(1+(0,25*a*t(i))^2)^0,5)]

Rachunek operatorów różniczkowych

Rozróżniamy następujące typy operatorów

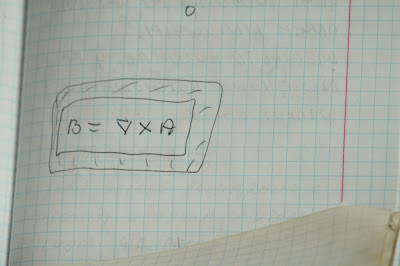
Operator Nabla daje współrzędne wektora a Laplasjan długość wektora. Łatwo to udowodnić stosując rachunek wektorów, który znajdziecie w tym blogu.

Następnymi bardzo ważnymi operacjami na tych operatorach jest
Rotacja z dywergencji
Dywergencja z dywergencji czyli przenikanie jest iloczynem skalarnym dwóch operatorów Nabla a rotacja iloczynem wektorowym dywergencji.  Teraz dwa ważne prawa

I
Rotacja z dywergencji równa się zero

Udowadniamy tą zależność rachunkiem tensorowym, który znajdziecie w tym blogu- Rachunek tensorowy.

II
Dywergencja z rotacji równa się zeru.

Wzór na rotację, który wyprowadzamy z rachunku tensorowego znajdziecie w artykule - Równania Maxwella podstawą teorii pola. Dipol elektryczny. Natężenie pola elektrycznego w odległości r od dipola. Zasada działania radia

policzymy tutaj natężenie pola elektrycznego E w odległości R od niego w punkcie P.Dipol drgający został umieszczony w postaci naładowanego pręta w kartezjańskim układzie współrzędnych wzdłuż osi Z. Korzystamy z zależności

Tutaj potencjał oznaczyliśmy po przez symbol fi, może bardziej szczęśliwe było by oznaczenie klasyczne U. Calka z pola eletrycznego jest potencjałem, więc skoro pochodna jest odwrotnością całki więc pochodna potencjału U daje pole elektryczne E.
Należy teraz określić potencjał pola elektrycznego fi w punkcie P. Tutaj zadanie jest proste gdyż potencjał ten jest różnicą potencjałów wynikających z odległości r1 = [0,0,-d/2] i r2 = [0,0,d/2], są to współrzędne r1 i r2. Innymi słowy to środek pręta znajduje się w układzie współrzędnych uczyniliśmy tak po to by zapewnić symetrię.

Kąt teta pokazany na rysunko jest kątem między osią Z a płaszczyzną X,Y.. Na tej płaszczyźnie został umieszczony środek dipola.. Wobec tego wypadkowy potencjał w punkcie P wynosi

Dla dużych odległości od dipola wielkość d^2/(4*r^2) jest tak mała, że możemy ją pominąć. Wyrażenie pod pierwiastkiem przybiera więc postać

Wobec tego wzór na wypadkowy potencjał w punkcie P przybiera postać

Następnie stosujemy przybliżenie pierwsze równanie na poniższym zdjęciu

Dla durzych r znowu człon w nawiasie możemy pominąć, więc ostatecznie wzór na potencjał w punkcie P, przybiera postać

Gdzie
P = Q*d _ moment dipolowy
d- rozmiar dipola
Q ładunek na dipolu
ponieważ Z/r = cos(teta), więc potencjał w punkcie P określony za pomocą r i teta ma postać

Pole elektryczne w odległości P od drgającego dipola

Chcąc policzyć pole elektryczne w punkcie P wracamy do wzoru określającego zależność pola elektrycznego od pochodnej potencjału. Parę zdjęć wyżej

Jest to wzór określający natężenie pola elektrycznego E w podległości r od drgającego dipola wyrażony za pomocą r - odległości i kąta teta
Chcąc policzyć pole elektryczne na osiach x,y,z wracamy do równania w postaci

Dla składowej Ez wykorzystaliśmy wzór na pochodną iloczynu dwóch funkcji>
Należy pamiętać, że te wzory są słuszne dla dużych r w porównaniu z rozmiarami dipola d. To koniec zadania , jak te wiadomości wykorzystać
Załużmy, że znamy odległość nadajnika radioewego i znamy też wzór określający zmianę pola elektrycznego, może to być przykładoeo
E = E0*cos(omega*T)
Wracamy teraz do równania Maxwela , znajdziecie je w tym blogu

Wzór na rotację też podaliśmy w tym blogu>
Licząc rotację a później całkując po czasie T powyższe równanie na E można policzyć pole B a następnie korzystając z prawa Ampera można policzyć natężenie prądu , który wyindukuje się w cewce radiowej

L - długość przewodnika cewki radiowej
Znając tą wartość można skonstruować wzmacniacz, który pozwoli nam słuchać audycji radiowych.

Prawo Biota-Savarta

W artykule Dipol elektryczny wyprowadziliśmy wzór na natężenie pola elektrycznego w odległości r od przewodnika. Przypomnimy ten wzór

Podstawiając za Q - ładunek wartość taką jak pokazaliśmy poniżej i obnirzając potęgę o jeden - to konieczność gdyż pole magnetyczne zależy od odwrotności odległości od źródła, otrzymamy

Otrzymujemy wzór na pole magnetyczne B w odległości r od przewodnika. Związek między ładunkiem a natężeniem prądu jest aksjomatem więc trzeba się tego nauczyć na pamięć. Pamiętajmy, że pole elektryczne E opisują ładunki Q a pole magnetyczne B natężenia prądów I. Zamieniając je tak jak pokazaliśmy wyżej otrzymujemy od razu wzory na pola odpowiednio E i B. Ponieważ dodaliśmy wielkość o wymiarze 1[m], wersor choć jednostkowy to jednak ma wymiar musimy podnieść r o jedną potęgę, to samo z polem elektrycznym.

Przechodząc do bardzo małych zmian i rozmiar dipola d zamieniając na bardzo małą zmianę przewodnika dL otrzymamy

Dalej z rachunku iloczynów wektorowych wiemy, że

Dodając więc wersor r pozbędziemy się sinusa, w ten sposób otrzymamy prawo Biota - Savarta w książkowej postaci.

Równanie falowe Równania Maxwela

Równanie takie wyprowadza się z równań Maxwela, na początek weźmy dwa z nich w postaci różniczkowej

Wprowadzimy pole A takie, że

Jest ono dowolne, a jedynym warunkiem jest to by jego całka równała się B. Z pierwszego równania otrzymujemy

Dla sumy takich pól możemy wprowadzić stały potencjał skalarny fi. Ponieważ mamy poprawej stronie równania zero więc korzystamy z rachunku pochodnych - Pochodna ze stałej równa się zero. Otrzymujemy w ten sposób

To równanie może posłużyć do wyprowadzenia równania falowego jednak to zostawiamy karzdemu czytelnikowi jako ćwiczenie. My tutaj wyprowadzimy równanie falowe na podstawie czwartego równania Maxwella

Dla jasności dodamy, że

Rachunek tensorów, bo z nim mamy do czynienia znajdziecie w tym blogu.

Przykład z propagacją fali dźwiękowej w ośrodku sprężystym. Prędkość rozchodzenia się fali Zauważymy, że operator różniczkowy

jest pochodną po współrzędnych liniowych. Wiedząc to rozpatrzmy falę rozchodzącą się wzdłuż osi x, równolegle do podłoża. Założymy jeszcze dla uproszczenia rachunków, że źródło fali znika po zadziałaniu a prpagacja fali zachodzi bez strat energetycznych. Rozpatrujemy wtedy równanie typu.

W danym ośrodku prędkość fali jest stała więc mamy równanie różniczkowe zerowego rzędu. Załużmy teraz ,że falę opisuje wzór, jest zgodny z rzeczywistością.

Niech teraz k będzie przedstawione jak na zdjęciu poniżej, sinusy i kosinusy zostały pominięte jako bardzo małe. Wyliczając pochodne względem x i t otrzymujemy

Zależność masy fali od masy ośrodka ciężko nam ująć we wzór zostawiamy to tęższym głową. Gęstość fali to masa tej fali zawarta w jej 1/2 długości lambda
Wyszła nam zależność odwrotnie proporcjonalna do gęstości a powinno być na odwrót, im większa gęstość tym większ prędkość fali. Można to łatwo skorygować, widać z powyższych równań, że prędkość fali jest odwrotnie proporcjonalna do k, należy przyjąć k takie jak na poniższym zdjęciu wtedy prędkość fali stanie się wprost prporcjonalna do gęstości

To teraz poprawna zależność Jednak pokusimy się o wyprowadzenie głębszej zależności. Gęstość fali to stosunek jej masy do zawsze stałej objętości tej fali. Masa zawarta w połówce fali w całości jest równa masie ośrodka, choć sama masa zmienia się jak cosinus alfa. Więc wzór na prędkość fali przybiera postać

Dla ciał stałych skorzystamy z zależności energii od ciśnienia

Ogólnie wzór na prędkość przybiera postać

w ciałach stałych energia fali wynikająca z ciśnienia i objętości , musi być równa energii elektrostatycznej, którą wytwarzają elektrony krążące na końcowych orbitach atomowych tworzące wiązania sieci krystalicznej. W tym przypadku Q jest ładunkiem elektronów a N jest liczbą elektronów brakujących do całkowitego obsadzenia orbity

Liczba 8 wzieła się z podstawienia za lambda , 1/2*lambda. jedna druga podniesiona do potęgi trzeciej daje jedną ósmą.
n - jest liczbą moli ciała stałego
k - jest stałą Boltzmana
T - jest temperaturą ciała stałego
k0 - stałą elektryczną
r.at-jest promieniem atomu do pierwszej nieobsadzonej do końca orbity
Dla cieczy sprawa jest prosta. Podstawiamy ciśnienie baryczne

Gdzie
q - gęstość cieczy lub gazu
g - przyśpieszenie planetarne
h - wysokość słupa cieczy
n - jest liczbą moli
k - jest stałą Boltzmana
T - jest temperaturą

Dla gazów należy podstawić P zmieniające się wraz z wysokością, łatwo znajdziecie je w internecie. Liczbę moli n liczymy ze wzoru

Gdzie
M.oś - masa ośrodka w którym rozchodzi się fala
m.at. - masa atomu wchodzącego w skład ośrodka

Długość fali do trzeciej potęgi daje objętość, która pomnożona przez gęstość ośrodka daje masę fali, zaś masa fali równa jest masie ośrodka. Otrzymujemy więc wzór

m - masa ośrodka w którym rozchodzi się fala.
Jest to nasze rozwiązanie być może niezbyt eleganckie gdyż wchodzi w nie długość fali. Istnieją rozwiązania pomijające tą wielkość

Prędkość i praca cząstek w gazach

Obliczamy ciśnienie wywierane przez cząstki na ścianki naczynia. Ponieważ cząski poruszają się chaotycznie, więc 1/3 cząstek będzie uderzała o każdą z par ścianek sześcianu. Cząstka zderzając się sprężyście dozna zmiany pędu
Zmiana pędu ciała jest równa pędowi siły

Czas przelotu między ściankami policzymy ze wzoru na prędkość

Ponieważ cząska porusza się tam i zpowrotem więc droga L = 2*L
Otrzymujemy więc układ równań

Dzielimy teraz obydwie strony równania przez powieżchnię ścianek by otrzymać ciśnienie

Jak wcześniej wspomnieliśmy 1/3 cząstek uderza w każdą parę ścianek, więc otrzymujemy wzór końcowy na ciśnienie uwzględniając, że pole powierzchni S razy odległość między ściankami L daje objętość sześcianu

Rozwiązując pierwsze równaie na zdjęciu względem v otrzymujemy wzór na prędkość cząstek gazu

Jest to bardzo zgrabne równanie, znając ciśnienie i gęstość gazu możemy policzyć prędkość cząstek a co za tym idzie i ich temperaturę korzystając ze wzoru
P*V = n*R*T
gdzie
n- liczba moli gazu
V-Objętość naczynia
T - Temperatura gazu

R - Stała Rytberga = 8,31 [J/stopień] Praca wykonana nad gazem

Przenosząc objętość na lewą stronę równania otrzymujemy zależność
P*V = E(k.śr)
Ponieważ energia jest równoważna pracy więc
Policzymy pracę dla premiany izobarycznej to znaczy takiej gdzie ciśnienie jest stałe a zmieniamy objętość. Oznacza to, że otoczenie doskonale odbiera temperaturę z naczynia z gazem, to znaczy temperatura też stała, tylko wtedy spełniony jest warunek stałości ciśnienia
Ponieważ zmieniamy objętość więc poniższe równanie całkujemy po objętości. Konieczna jest znajomość racunku całkowego oraz rachunku logarytmów. Wszystko to znajdziecie w tym blogu.

Jest to praca na n molach gazu
Pracę na jeden mol gazu otrzymamy dzieląc powyższe równanie przez n

Też bardzo zgrabne równanie. Powinno być przed całością razy 1 [J]
Zapomnieliśmy dodać stałą całkową C. Z warunków początkowych otrzymujemy V1=V2, gdyż na początku nie wykonano pracy.

We wzorze na pracę po prostu tej jedynki niezapisaliśmy, jednak stale należy o niej pamiętać, gdyż ma wymiar energii. otrzymujemy ln(1) po czym korzystamy z aksjomatu sumy logarytmów

Budowa i zasada działania transformatoraj

Transformator składa się z dwóch uzwojeń, pierwotnego Z1 i wtórnego Z2, Połączonych frromanetykiem, który spełnia rolę przewodnika pola magnetycznego B. Przepływ prądu zmiennego w cewce Z1 powoduje indukcję pola magnetycznego, które jest przewodzone przez ferromagnetyk, innymi słowy ferromagnetyk drga tym wyindukowanym polem magnetycznym. Ponieważ drga cały więc te drgania w cewce Z2 powodują indukcję prądu o natężeniu I2. Indukcję prądu przez zmienny prąd opisaliśmy tutaj

http://jakpowstajfraktale.blogspot.com/2012/03/prawa-naturalne-fizyka-w-piguce-dla.html

Załóżmy teraz, że ustalamy długość przewodnika cewki a zmieniamy tylko pole powierzchni, Zauważmy przy tym, że pole powieżchni delta s razy długość przewodnika daje objętość przewodnika. By nie doszło do rezonansu w kondensatorze, móże być on konstruktywny bąź destruktywny, ustala się taką samą objętość dwóch cewek po przez odpowiedni dobór średnicy przewodnika, zyskuje się tym sposobem różnicę w ilości uzwojeń n. Rozwiązując powyższy układ równań względem I oraz pamiętając, że objętości dwóch cewek są sobie równe oraz czasy delta t drgań są takie same otrzymujemy

Dzieląc I1 i I1 przez siebie otrzymujemy klasyczny wzór zwany przełożeniem transformatora. Przez pomyłkę pomineliśmy delta t na powyższym zdjęciu, jednak skoro są równe to i tak się skracają

Wyprowadzenie prawa Ampera - Prawo Ampera

Prąd o gęstości j płynie przez przewodnik wzdłuż osi Z. Związek między gęstością a natężeniem prądu został pokazany na poniższym zdjęciu. Jest to prawo aksjomatyczne trzeba zrozumieć i zapamiętać.

Korzystamy z pierwszego równania Maxwella

Całka i operator różniczkowy dywergencji znoszą się, gdyż całkowanie jest odwrotnością różniczkowania, nie wolno tak robić w przypadku rotacji. Otrzmujemy więc równanie na natęrzenie pola elektrycznego E

Po uwzględnieniu wzoru na Q otrzymujemy

Drugie równanie na zdjęciu pokazuje związek między potencjałem i polem elektrycznym E. Później zrozumiecie po co liczymy tą wielkość. Dalej mamy

W artykule- Równanie falowe i prawa maxwela - wprowadziliśmy pole A którego rotacja daje pole magnetyczne

Tutaj wyprowadzone pole fi jest właśnie odpowiednikiem pola A i stanowi jego potencjał tak jak V jest potencjałem pola elektrycznego E. Jest to bardzo warzny wzór, nauczciesię dobre sposobu wyprowadzenia, Tak więc pole magnetyczne B jest rotacją pola potencjalnego fi.

Przypomnimy tutaj operator rotacji, Oprator rotacji od dywergencji różni się tylko iloczynami, pierwszy jest iloczynem skalarnym drugi iloczynem wektorowym, to daje olbrzymią różnicę. Wzór na rotację otrzymuje się z rachunku tensorowego, który znajdziecie w naszym blogu, wzory na dywergencje i rotację pola podaliśmy terz w artykule- Równania Maxwella podstawą teorii pola- Też znajduje się w tym blogu< oto wzór na rotację

We wzorze tym na przykład f(z) - oznacza, że składową zetową pomijamy we wzora, pozostaje tylko x i y.
Ponieważ prąd płynie tylko po składowej Z Więc niezerowe rozwiązanie istnieje tylko dla składowej fi(z), wszystkie inne sięzerują pokazaliśmy to na poniższym zdjęciy. Pamiętajmy , że ze wzoru na
r^2= x^2+y^2+z^2
składową z^2 odrzucamyzostaje więc pocodna po y i po x tylko z równania
r^2 = x^2+ y^2

Korzystając z twierdzenia logarytmów 1/2 wynosimy przed logarytm i stosujemy wzór na pochodną funkcji złożonej. Mając składowe Bx, By,, Bz, korzystamy z twierdzenia Pitagorasa, które da nam wypadkowy wektor B pola magnetycznego

Przenosząc L na lewą stronę równania i przechodząc z l na d(L), otrzymamy klasyczne prawo Ampera w postaci całkowej

d(L) - jest dowolną krzywą przedstawioną dowolnym wzorem, może być to po prostu L lub np. L*ln(L)
Zauważmy, że przenikalność próżni razy prędkość światła do kwadratu daje przenikalność magnetyczną próżni, ściślej jej odwrotność. Jeżeli przeniesiemy 2*pi na lewą stronę wtedy otrzymamy całkę obrotową, która jest ostateczną postacią prawa Ampera

Pierwsze i drugie prawo Keplera

I prawo Keplera
Ruch planet odbywa się po torach eliptycznych, gzie w jednym z ognisk elipsy leży Słońce.

II prawo Keplera
Promień wodzący planety zakreśla w równych odstępach czasu równe pola. Inaczej mówiąc prędkość polowa planet jest stała.

Dowód drugiego prawa Keplera

Prędkość polowa będzie zmianą pola zakreślonego przez planetę do czasu w którym to ple zostało zakreślone. Rysujemy wykres i układamy mikro równanie

Ponieważ jak widać na poniższym zdjęciu chodzi nam o dS, więc wielkość tą wyciągamy spod całki.

Skorzystamy teraz z prawa zasady zachowania momentu pędu L

Widać, że prędkość polowa zależy tylko od momentu pędu L, który jest stały, więc i prędkość polowa jest stała, co należało udowodnić

Dynamika relatywistyczna - Wyprowadzenie wzoru na przyśpieszenie relatywistyczne

W dynamice relatywistycznej często występuje wielkość, nadano jej osobny symbol

I tak droga, czas i masa transformują się według wzorów, im v bliższe prędkości światła c tym wyraźniejsze efekty relatywistyczne

Więcej na ten temat znajdziecie w tym blogu
Żeby określić przyśpieszenie relatywistyczne posłużymy się wzorem

Ponieważ gamma zależy od prędkości więc stosujemy wór na pochodną iloczynu funkcji

Dalej przyglądnijmy się członowi tego równania

Dalej pomnożymy ten człon i podzielimy przez prędkość światła do kwadratu

Dalej łączymy obydwa człony

Podzielimy teraz obydwie strony równania przez m otrzymując w ten sposób przyśpieszenie relatywistyczne

Energiia relatywistyczna - Wyprowadzenie wzoru

By określić energię relatywistyczną rozpatrzmy równanie zmiany tej energii w czasie. Łatwo sprawdzić, że pochodna energii po czasie równa się sile pomnożonej przez prędkość.

Wyliczamy d(E) po przez rozdzielenie zmiennych

Stosujemy teraz wzór na całkę iloczynu dwóch funkcji, łatwo znajdziecie go w internecie. Wgląda to następująco

Czasy skróciły się więc całkujemy po prędkości.Całka ta daje energię kinetyczną, zapiszmy ją w postaci energii całkowitej a jej wartość będzie zależna od zmiany gama a ściślej wchodzącej w jej skład wielkości beta
                                                                                 

Skorzystamy teraz z twierdzenia Pitagorasa, współrzędne skalara energii podniesione do kwadratu dadzą wypadkowy skalar.

Otrzymaliśmy wzór na energię relatywistyczną, a wzór na pęd relatywistyczny otrzymamy rozwiązując pierwsze równanie względem P.

Są to wzory różniące się od oficjalnie przyjętych. Czy są poprawne tego nie wiemy. Proponujemy tę nieścisłość wyjaśnić na wykładach.

Wyprowadzeniewzorów na liczbę zderzonych cząstek, Kąt bryłowy rozproszenia cząstek, Przekrój czynny na zderzenie cząstek - Przeszkody. Przekrój czynny Rutherforda

Liczba zderzonych cząstek w przeszkodzie
Prawdopodobieństwo zderzenia cząstki z atomem przszkody jest określony aksjomatycznie w postaci

Następnie wprowadzimy pojęcie średniej drogi swobodnej cząstek w przeszkodzie którą przebędzie cząstka w przeszkodzie zanim dojdzie do jej zderzenia z atomem przeszkody

Przenosząc na prawą stronę fi zero i uwzględniając wzór na średnią drogę swobodną otrzymujemy

Liczba zderzonych cząstek N jest równa różnicy strumienia cząstek przed przeszkodą i za przeszkodą

Z definicji aksjomatyczej średniej drogi swobodnej otrzymujemy

Wyprowadzenie wzoru na kont bryłowy prawdopodobieństwa rozproszenia zderzonych cząstek w przeszkodzie.

Prawdopodobieństwo rozproszenia w kąt bryłowy omega jes aksjomatycznie określony następująco

Wyprowadzenie wzoru na przekrój czynny atomów przeszkody

Można też kąt bryłowy prawdopodobieństwa zdefiniować następująco

Stąd zmiana przekroju czynnego wynosi

Dalej należy określić przekrój czynny zależny od strumienia fi i prędkości cząstek padających na przeszkodę. Można wykorzystać w tym celu wcześniej wyprowadzony wzór na liczbę N zderzonych cząstek, jednak możemy rozpatrzyć problem bardziej dokładnie. W tym celu zastosujemy zasadę zachowania momentu pędu rozproszonych cząstek i wprowadzimy promień b zwany parametrem zderzenia, Wystarczy spojrzeć na pierwszy rysunek i zamiast R dopisać sobie b , który będzie się zmieniał w zależności od gęstości strumienia cząstek padających na przeszkodę i w zależności od ich prędkości.

,br> Zauważmy następnie, że zmianie b o d(b) musi towarzyszyć zderzenie co pomnożone przez grubość przeszkody x da liczbę jąder w przeszkodzie, b*d(b) po to by po scałkowaniu otrzymać pole powierzchni.

Zmianę liczby zderzonych cząstek w zależności od ich prędkości możemy określić w następujący sposób

W ten sposób otrzymaliśmy wzór na przekrój czynny zależny od gęstości strumienia cząstek padających na przeszkodę wyrażony za pomocą prędkości tych cząstek, Inaczej wany Przekrojem czynny Rutheforda

Fizyka jądrowa. Wyprowadzenie wzoru na liczbę stanów kwantowych, pęd i energię i siłę jądrową- jądra atomowego.

Znajdziemy tutaj wzory na liczbę stanów kwantowych, pęd i energię- jądra atomowego w zależności od liczby N nuklidów - protonów i neutronów- i promienia R tego jądra.
Jak wiemy z elektrostatyki dwa jednakowe ładunki odpychają się, jednak gdy zbliżyć je do siebie na odpowiednią odległość, wtedy do głosu dochodzą silniejsze siły przyciągające, zwane siłami jądrowymi. Jej energia jak się dalej przekonamy, zależy tak jak dla ładunków odwrotnie od promienia jądra, jednak zamiast ładunku istnieje masa protonu w mianowniku, co determinuje ogromną energię wiązań jądrowych..
Wraz ze wzrostem promienia jądra, energia ta maleje gdyż masa nukleonu jest ustalona. Tym samym sytuacja jest niemal odwrotna niż w elektrostatyce, w niej ładunki się sumują a suma ta jest podniesiona do kwadratu gdy chodzi o energie i siły. Skutkiem tego siły jądrowe choć o wiele wiele potężniejsze od elektrostatycznych, mają bardzo krutki zasięg.
Wyprowadźmy teraz wzór na tą energię. W tym celu wykożystamy postulat Bohra

gdzie n jest kwantem, liczbą całkowitą o którą mogą zmieniać się momenty pędów elektronów krążących po orbitach atomowych. założymy teraz, że w jądrach atomowych jest tak samo, czyli liczba możliwych pędów neutronów i protonów w jądrze jest też skwantowana..
Dalej będziemy rozpatrywać objętość przestrzeni pędów i wielkości liniowych, to konieczne, gdyż całkowita liczba możliwych pędów tworzy pewną przestrzeń. W tym celu równanie Bohra podniesiemy do trzeciej potęgi.

n - niepodnosimy do trzeciej potęgi, gdyż liczba możliwych stanów w przestrzeni jest dalej n.
h^3 - daje sześciowymiarową przestrzeń we współrzędnych, Px,Py,Pz i w przestrzeni liniowej, x,y,z.Stąd łatwo wyliczyć n - możliwą liczbę stanów jądra.

Dalej z zasady Pauliego wiemy, że jeden stan mogą obsadzić dwa nuklidy o przeciwnych stanach, powyższy wzór przedstawia taką sytuację, więc dzieląc ten wzór przez 2 otrzymamy ilość protonów i neutronów w jądrze.

Jest to wzór na pęd w zależności od liczby protonów i neutronów w jądrze. Dalej zauważymy, że

gdzie r0 - promień protonu lub neutronu. Podstawiajć to otrzymujemy

Podstawiając ten pęd do wzoru na energię mamy dalej końcowy wzór

Pamiętajmy, że pochodna energii po drodze daje siłę, tutaj trzeba policzyć pochodną po d(r) i d(N) W tym celu trzeba uzmiennić r0 po przez pomnorzenie przez N, wtedy wzór na energię przybiera postać

a na siłę jądrową

Widać wyraźnie, że siła zależy od odwrotności promienia w trzeciej potędze. To daje olbrzymie różnice między siłą Kulombowską i jądrową ta ostatnia dla małych R jest dużo większa a dla dużych dużo większa.

                        http://jakpowstajfraktale.blogspot.com/