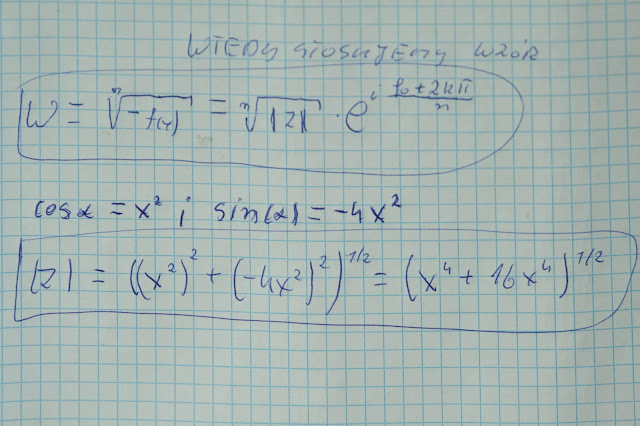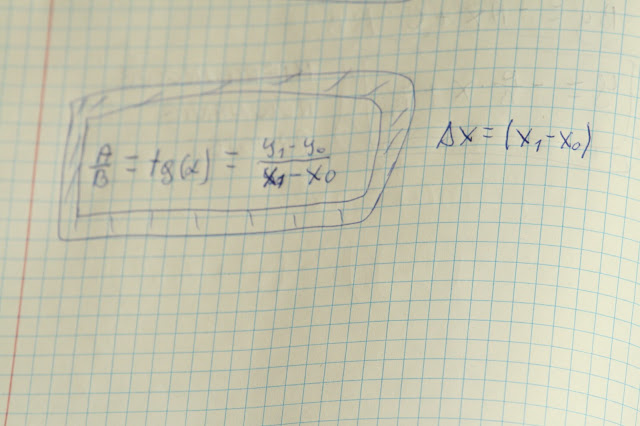Tajemnicza matematyka - Rodzaje funkcji - Podstawowe operacje na funkcjach
Las matemáticas misteriosas - Tipos de funciones - Operaciones básicas sobre las funciones
Los axiomas de la matemática, física y espiritual. Consejo práctico.
Aksjomaty matematyczne, fizyczne i duchowe. Rada praktyczna.
Nie jest najważniejsza umiejętność tworzenia skomplikowanych reguł wynikających z aksjomatów podstawowych. lecz dowód logiczny wraz z doświadczalnym i pamięć, tych że aksjomatów.
Drogi czytelniku, ile czasu zajmie Tobie sprawdzenie czy lewa strona aksjomatu podstawowego równa się prawej. Wydaje się, że jest to błaha sprawa jednak tak naprawdę jest to najważniejsze. Dowód taki przeprowadzamy własnoręcznie bez pomocy kalkulatorów i komputerów, co na przykład w przypadku aksjomatów logarytmów będzie trudne. Udowodnienie sobie aksjomatu podstawowego powoduje jego zapadnięcie w Naszą Pamięć. W sytuacji gdy mamy do czynienia ze złym Bogiem, który jest naszym Ojcem, nie podążajcie po skomplikowanych zależnościach logicznych na siłę, chyba że sprawia Wam to przyjemność, gdyż po pewnym czasie zapomnimy drogę logiczną. Udowodnionego raz aksjomatu podstawowego nie Jest On Nam wstanie odebrać. Należy ćwiczyć zdolność kombinowania od podstaw logicznych.-
Wstęp
Kto dopiero zaczyna naukę matematyki, lub ma poważne trudności ze zrozumieniem tego bloga,dobrze trafił. Żeby módz żąglować wzorami, potrzebne są pewne aksjomaty, co w przełożeniu na nasze, oznacza podstawy, których nie trzeba udowadniać, które po prostu są gdyż taka jest natura rzeczy. Takich podstaw nie jest dużo, w porównaniu do korzyści jakie odniesiemy z ich znajomości, opłaca się włożyć co prawda nie mały wysiłek w ich naukę. Proponujemy wykonać dużo działań na tych podstawach, tak by zapadły w pamięć i pod świadomość, dopiero później można ruszyć dalej.
Rozwój czakr ziemskich powinien iść w parze z rozwojem czakr duchowych, i dla nich istnieją podstawowe aksjomaty, które należy w tym przypadku zrozumieć. Dlatego polecamy na wstępie przeczytać też poniższy artykuł
Podaję też link do strony zrzeszającej korepetytatorów by zapromować tą stronę. Kto chce zapłacić za naukę znajdzie tam coś dla Siebie.
http://www.twojekorki.pl/korepetycje/matematyka_trzebinia_e323032363a38.html
Aksjomaty matematyczne
Prawa aksjomatyczne to prawa, które niepodlegają dowodzeniu. Wobec tego prawa te należy nauczyć się na pamięć. Mówiąc dosadnie wkuć je tak by umieć w nocy o północy, by zapadły w pod świadomość. Bez zapamiętania tych aksjomatów droga do matematyki i innych przedmiotów ścisłych jest zamknięta. Do kompletu należy jeszcze zapamiętać wzory na upraszczanie skomplikowanych funkcji, które znajdziecie tutaj
i można zgłębiać tajniki matematyki wyższej.
Podstawowy aksjomat sprowadzania do wspólnego mianownika
Przykład
To naszym zdaniem najważniejszy aksjomat. Bez niego nie można by było upraszczać równań. Nie można też by było w większości przypadków wyliczać niewiadomych z tych równań
Aksjomat dzielenia ułamka przez ułamek
Podzielić ułamek przez ułamek to to samo co pomnożyć pierwszy ułamek przez odwrotność drugiego
Na powyższym zdjęciu jest szkolny błąd, którego niezauważyliśmy. To dowód jak bardzo zły nas kontroluje. Tym samym Wy ucząc się matematyki będziecie narażeni na jego ataki. Poprawny wynik, który dodaliśmy po paru dniach od powstania tego artykułu pokazaliśmy na zjęciu poniżej.
Aksjomaty funkcji trygonometrycznych
Są to wprowadzone wielkości opisujące trójkąt, które potwierdzono doświadczalnie. To też aksjomaty i trzeba nauczyć się ich na pamięć.
To że suma kwadratów sinusa i kosinusa równa jest jeden, Wielokrotnie potwierdzono doświadczalnie i takie doświadczenie każdy sam może sobie przeprowadzić mierząc trójkąty o różnych bokach a i b. Mając dwa trzy udowodnione równania, można już przeprowadzać na nich kolejne kombinacje. Pokażemy tu jedną.
Wyrazimy tg za pomocą kosinusa
Aksjomaty działań na równaniach znajdują się niżej. Są bardzo ważne.
Aksjomaty działań na równaniach
Na równaniach możemy wykonywać następujące operacje
1
Przenosić całe wyrażenia lub liczby pojedyncze z jednej strony na drugą ze zmienionym znakiem
Przykład przeprowadzimy na samych liczbach. Rozpatrzmy takie równanie
2+2 = 4
Jest ono prawdziwe, gdyż lewa strona równa się prawej. Przenieśmy teraz zgodnie z tą zasadą dwójkę na prawą stronę
2 = 4 - 2
2 = 2
Po takiej operacji też otrzymaliśmy prawdziwe równanie, prawa strona równa się lewej
2
Obustronnie mnożyć równanie przez tą samą liczbę
3
Obustronnie dzielić równanie przez tą samą liczbę
4
Obustronnie podnosić równanie do tej samej potęgi
5
Wyciągać przed nawias wspólny czynnik Np.
2*x^2 -3*x = 5
Wspólnym czynnikiem jest x wtedy
x*(2*x - 3) = 2
Po wymnożeniu nawiasu otrzymamy poprzednią postać równania,
Czyli dokonaliśmy operacji upraszczającej to równanie a nie zmieniającej.
5
Obustronnie logarytmować równanie przez ten sam logarytm
Przykład
Dowód
W tym przykładzie dodaliśmy i jednocześnie odjęliśmy y. Wykorzystałem następujący aksjomat
Oraz aksjomat wyłączania wspólnego czynnika przed nawias, którym w podanym przykładzie jest x^2.
W paru słowach płęta. Możemy wykonywać na równaniach takie działania by równanie którego lewa strona równała się prawej ( w przeciwnym przypadku równanie jest fałszywe np. da wynik 2 =3 co jest widoczną nieprawdą), po zadziałaniu na niego w wyżej opisany sposób dalej było prawdziwe, to znaczy by dało wynik np. 2 =2. Trzeba przede wszystkim nauczyć się tych aksjomatów, gdyż gwarantują one prawdziwość równań, przed i po operacji na nich
Przykład
Aksjomaty potęg
Aksjomaty logarytmów
Logarytm jest odwrotnością funkcji
c= a^b
wprowadzono więc na tej podstawie funkcję zwaną logarytmem, taką, że
b = loga(c)
funkcja o podstawie e, która jest liczbą równą
e = 2,781,,,,,
Występuje tak często w matematyce, że nadano jej specjalny symbol
loge = ln
Liczby a i e nazywamy podstawą logarytmu.
Poniższe zdjęcie pokazuje opracje na logarytmach, ich tożsamości i jak wyżej wspomnieliśmy trzeba nauczyć się ich na pamięć
Po przez ln występujący na zdjęciu rozumiemy log o podstawie a i b, Zrobiliśmy to po to by się przyzwyczaić do oznaczenia ln jest to wyjątkowy logarytm po przez bardzo częste występowanie.
Znając te aksjomaty możemy udowodnić działania na potęgach
Logarytmy typu log o podstawie a występują w matematyce i w fizyce sporadycznie.
Liczby a, b i c są dowolnymi liczbami. tylko symbol e jest zarezerwowany dla liczby 2,781....
To samo tyczy się liczb zespolonych gdzie liczba urojona (i) podniesiona do kwadratu daje -1, a którą wprowadzono aksjomatycznie. We wszystkich pozostałych przypadkach ujemna liczba podniesiona do kwadratu daje liczbę dodatnią.
Sama liczba (i) nie ma wartości liczbowej, dopiero jej kwadrat daje -1. Moduły we wzorach, w których występuje (i), nie bierzemy pod uwagę, jednak zostawiamy te moduły gdyż w dalszych podstawieniach, do innych wzorów (i) może wystąpić w kwadracie, co da jej wartość -1. Np.
y = a*x +i^2*x^2 = a*x+(-1)*x^2 = a*x - x^2
Po podstawieniu iksa wynikiem liczbowym takiej funkcji jest tylko moduł a*x
Liczbie zespolonej nadano symbol
Z = a - i*b
Została wprowadzona aksjomatycznie, gdyż zaobserwowano w przyrodzie zjawiska, które znikają w przewidujących je równaniach, a pozostają tylko wtedy gdy wprowadzi się liczbę urojoną (i).
Znak minus wprowadzono po to by uzyskać płaszczyznę zespoloną.
Łatwo sprawdzić, że liczba sprzężona do liczby zespolonej równa
Z* = a+i*b
Która też została wprowadzona aksjomatycznie
do liczby zespolonej, razy liczba zespolona daje
Z x Z* = a^2 + b^2 = R^2
A ponieważ jest to twierdzenie Pitagorasa więc wielkość ta równa się R^2 czyli promieniowi okręgu na płaszczyźnie.
Na osi y zaznaczamy a , zaś na osi x zaznaczamy i*b,tak jak pokazaliśmy na poniższym zdjęciu.
Kolejnym wzorem wprowadzonym aksjomatycznie dla liczb zespolonych jest wzór pokazany niżej
Jest to najprawdopodobniej aksjomat, trzeba nauczyć się go na pamięć.
na powyższym zdjęciu sinus i kosinus powinny być w nawiasie, przepraszamy za błąd.
Twierdzenie More"a
Przykład
Twierdzenie
Itstneje dokładnie n pierwiastków liczby pod pierwiastkiem stopnia n, i wyrażają się one wzorem :
Należy jeszcze dodać, że moduł liczby z jest wartością bezwzględną więc zawsze dodatnią
Przykład
Każdą liczbę można przedstawić za pomocą pierwiastka
Wyraźnie widać, że ten wzór stanowi nadbudowę do rozwiązania równań kwadratowych a ogólnie n - tego stopnia, gdy n jest całkowite dodatnie, tu mamy uzupełnienie o potęgi ułamkowe.
Bardzo potężny wzór
Trzeba się po prostu nauczyć tego na pamięć, to tylko parę wzorów na Z i Z*, cała reszta wynika z logicznych zależności
Trzeba się po prostu nauczyć tego na pamięć, to tylko dwa wzory na Z i Z*, cała reszta wynika z logicznych zależności
Załóżmy teraz, że opisujemy matematycznie jakieś zjawisko i wyszedł nam trój mian kwadratowy, którego delta jest mniejsza od zera. Oznacza to, że nie ma rozwiązania takiego trójmianu, jednak w przyrodzie występuje takie zjawisko, co wtedy robić. Wzoru jesteśmy pewni. Przykład podajemy na poniższych zdjęciach
Pamiętamy, że
e^(i*fi) = cos(fi) + i*sin(fi)
Co w połączeniu ze wzorami
Daje kompletne rozwiązanie. sinus plus kosinus wstawiamy za e^(i*fi), a f(x) jest naszą funkcją, która nie dała rozwiązania w dziedzinie liczb rzeczywistych.
Daje kompletne rozwiązanie. sinus plus kosinus wstawiamy za e^(i*fi), a f(x) jest naszą funkcją, która nie dała rozwiązania w dziedzinie liczb rzeczywistych. d(f(x))/d(x) - jest pochodną tej funkcji, żeby się dowiedzieć o pochodnych zapraszm na naszą stronę
www.latwa-matematyka.blogspot.com
Części urojonej, to znaczy części wzoru w którym występuje czynnik (i) nie bierzemy pod uwagę. Rozwiązaniem jest tylko część rzeczywista, jednak części urojonej nie odrzucamy przy dalszych podstawieniach do innych wzorów. Podstawiamy cały wzór.
ASJOMATY DZIAŁAŃ NA WEKTORACH
Też trzeba nauczyć się na pamięć. Podaliśmy tu wzory na sumę iloczyn długość sinus konta alfa i kosinus między wektorami.
Aksjomat mnożenia wektora przez wektor jest dziwnym co najmniej aksjomatem.
a+b wcale nie równa się a*b, gdzie za a i b podstawiamy dowolne liczby. Tym samym można go traktować jako przybliżenie, choć ja znam lepsze. Oto oto ono
Moim zdaniem powinno być
Poniżej zamieszczam wykres dla
a = [3 ; 2]
b = [4 ; 3]
Wynik powinien być równy 12,04. Przepraszam za błąd.
To potraktujcie jako ciekawostkę nie radzę podawać go jako prawdziwe na kolokwiach czy klasówkach gdyż wrócicie z dwóją
MOŻECIE TERAZ PRZECZYTAĆ ARTYKUŁ - BŁĄD WSZECHŚWIATA.
tym samym wzory podanie niżej na sin i cos pomiędzy dwoma wektorami, trzba by było uzupełnić o podaną wyżej zależność
Wzory aksjomatyczne na sinus i kosinus między osią x
Tu taj wzory na kosinus i sinus tyczą się kąta między osią x
Wzory na sinus i kosinus między dwoma wektorami
We wzorze na cos, powinno być
a1*b2 + a2*b1
Jednak należy pamiętać, że wzór na cosinus przyjęty przez oficjalną naukę jest w formie podanej na zdjęciu poniżej.
Twierdzenie kosinusów
Dotyczy ono sytuacji gdy mamy trzy wektory, Tak jak pokazano na poniższym zdjęciu.
By twierdzenie było prawdziwe, wektory a i b muszą być skierowane przeciwnie do siebie, tak jak poazałem na powyższym zdjęciu. Zachodzi wtedy równość
c = a-b
Stąd c^2
Koniecznie musi być spełniony warunek c = a-b!!!!!!!!!!!!!!!!!
Jeżeli nie jest nie wolno stosować tego wzoru.
Koniec aksjomatów, chyba podałem wszystkie najbardziej podstawowe. Teraz skorzystamy z nich by wyprowadzić ogólne i kierunkowe równanie prostej.
Do ogólnego równania prostej dochodzimy startując z definicji kosinusa między wektorami. Z kosinusa dlatego by dwa wektory miały część wspólną, bu przecinały się ze sobą. Zakładamy warunek początkowy taki, że dwa wektory są do siebie, to oznacza kont prostopadłe, zauważmy, że taki warunek oznacza kąt równy 90 stopni a to z kolei pociąga za sobą fakt iż cos(90) = 0

Nigdy nie wolno dzielić przez zero gdyż taki cosinus ma granicę niewłaściwą w nieskończoności. Dlatego licznik przyrównujemy do zera
Sporządzimy sobie następujący schemat
Zakładamy, że współrzędne x0 i y0 są znane oraz znane są współrzędne A i B. Wektor delta(P) ma współrzędne
delta(P) = [(x-xo) ; (y-y0)] = [b1 ; b2]
i odpowiednio A = a1 i B = a2
Podstawiamy to do pierwszego równania otrzymanego z definicji kosinusa
Ponieważ xo i yo są punktami zaczepienia znanymi więc
A*xo-B*yo = c stałej. Stąd ogólne równanie prostej przechodzącej przez punkt o współrzędnych [A ; B] ma postać
Jest to Ogólne Równanie Prostej.
W ten sposób nierozerwalnie połączyliśmy ze sobą prostą i punkt (a). Ponieważ założyliśmy cos = 0 więc mamy pewność, że punkt a leży na prostej wyznaczonej przez dwa punkty, którym drugim punktem jest punkt P.
Kierunkowe równanie prostej
Otrzymujemy przez zwykłe rozwiązanie równania względem y
Jeżeli teraz będziemy zmieniać A,B x i y, będziemy tym samym obracać wektor P a więc i prostą na której leży. Po rozwiązaniu względem y otrzymujemy kierunkowe równanie prostej
a zmiana delta(y) która wynika ze zmiany A;B y i x wynosi
Z podanych wyżej wykresów możemy napisać równość
Wstawiając to do równania na delta(y) i pamiętając, że delta(y) = y - yo najogólniej, otrzymamy
Jest to równanie kierunkowe prostej
Powtórzymy tą czynność jeszcze ra, to znaczy znowu zmieniamy x a co za tym idzie zmienia się i y. Możemy więc napisać
Stąd już tylko krok do pochodnej
Pochodną zajęliśmy się na stronie
www.latwa-matematyka.blogspot.com
My tutaj wrócimy do równania, które jest funkcją liniową. To pierwszy rodzaj funkcji
Przykład zastosowania
Napisz równanie prostej przechodzącej przez punkty
P = [1;2]
a = [6;7]
Sprawa jest prosta podstawiamy współrzędne do równania kierunkowego prostej
Należy zapamiętać ważny wniosek. Pierwsza współrzędna punktu to x a druga to y. Natomiast jest odwrotnie gdy zaznaczamy punkty na wykresie, tak więc w równanie wstawiamy pierwsze x drugie y a przy zaznaczaniu punktów na wykresie odwracamy, pierwsze jest y drugie x. Dlaczego tak jest pozostaje dla mnie tajemnicą!!!!! Może wyciągnąłem błędne wnioski odnośnie tego problemu, prawda sama się broni, więc niech każdy czytelnik udowodni to sobie po rzez rysowanie wykresów otrzymanych prostych.
Zauważmy, że a - jest tangensem konta nachylenia tej prostej względem osi x Zadajmy sobie pytanie, jak z taką informacją wyliczyć równanie prostej prostopadłej do uzyskanego wyżej równania?. Wtedy to nastąpi gdy (a2) będzie odwrotnością tangensa (a) i będzie ujemne to znaczy, że ich iloczyn równy jest minus jeden.
Warunek prostopadłości wektorów i prostych
W naszym równaniu prostej a = 1, więc a2 = 1/a = - 1. wstawiamy to za a w naszym równaniu i otrzymujemy drugie prostopadłe do pierwszego.
Jak otrzymać teraz równanie równoległe do pierwszego? Otóż wystarczy zmienić w tym równaniu stałą c. Gdy zaś mamy wektory np.
a = [-3;2]
b = [5;4]
c = [1;2]
d = [5;3]
a,b,c,d są punktami o współrzędnych takich jak pokazano, to zakładamy, że wektory powstałe z tych punktów są równoległe. Sięgamy do aksjomatów działań na wektorach.
Mogli byśmy założyć cos = 0 jednak w takim przypadku otrzymamy dwa wektory pokrywające się ze sobą, leżące na jednej prostej. sins jest równy zero dla kąta równego 90 stopni i oto nam chodzi. Otrzymamy wtedy wie proste równoległe oddalone od siebie. Dalej w formie zdjęć
Na koniec zapamiętajmy, iż różnica współrzędnych na we wzorach na sinus i kosinus jest aksjomatyczna.
Funkcja kwadratowa
Otrzymujemy ją z pomnożenia dwóch dowolnych funkcji liniowych.
Można ą doprowadzić do tak zwanej postaci kanonicznej
f(x) = a*(x+k)^2 + d
gdzie k id będzie wyrażone znanymi stałymi a b c. Ktoś to przepięknie zrobił na jednej ze stron, podaję adres:
Wobec tego równanie truj mianu kwadratowego ma postać
Zero w matematyce jest szczególną liczbą bardzo upraszczającą równania. Jeżeli powyższe równanie przyrównamy do zera i rozwiążemy je względem x to otrzymamy liczby w których funkcja f(x) jest równa zeru, to znaczy przecina oś x.
Bardzo często rozwiązując jakieś równania otrzymujemy ich postać typu
a*x^2 + b*x + c = 0
Przyrównajmy więc powyższy truj mian do zera i otrzymamy wtedy gotowe wzory na x czyli rozwiązanie szukanej wielkości.
Pamięŧąjmy
Równanie kwadratowe f(x) = x^2, ma zawsze dwa rozwiązania + i -. Np.
Powodem tego jest symetryczność, parzystość funkcji kwadratowej, ujemna liczba podniesiona do kwadratu daje liczbę dodatnią, to jest powód dwóch rozwiązań. Wykresem funkcji kwadratowej jest parabola, dla truj mianu również. Dla powyższego przykładu wykres wygląda następująco;
a = 1 ; b = 0 ; c = 4.
Mamy więc rozwiązanie x-ów. Przypatrzmy się jeszcze raz równaniu kwadratowemu w postaci
Jeżeli podstawimy do tego równania wyliczone x to otrzymamy wartość f(x) w punkcie x(1;2), czyli wierzchołek paraboli
Co zachodzi tylko wtedy gdy delta równa zero. Gdy delta równa zero, wtedy mamy jedno miejsce zerowe, które pokrywa się z wierzchołkiem paraboli. Tym samym mamy wzór na wierzchołek paraboli.
Mamy w ten sposób x i y a więc współrzędne wektora a równania kwadratowego. Powinno być f(-b/(2*a)).
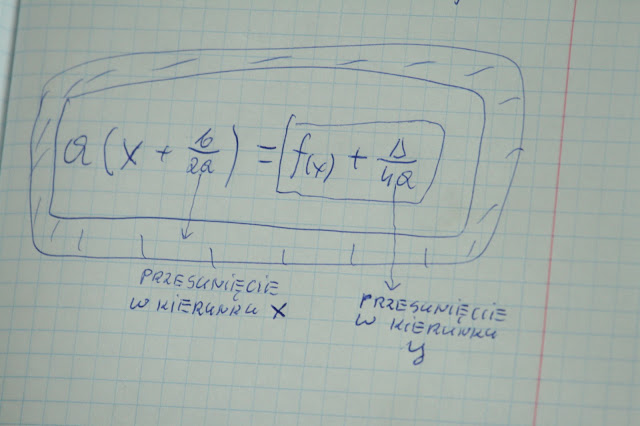
Najprościej jak mogę to wytłumaczyć w inny sposób. Z równania kwadratowego w postaci kanonicznej widać, że wierzchołek paraboli w kierunku x jest przesunięty o -(b/(2*a)) a w kierunku y o -(delta/(4*a)).
Najdokładniej widać to w równaniu jeżeli nie przyrównamy je do zera, wtedy mamy go w ogólnej postaci dla każdego a,b,c, jeżeli teraz przeniesiemy -(delta/(4*a)) na stronę f(x) wtedy te przesunięcia będą wyraźnie widoczne. Pokazuję to na poniższym zdjęciu
Najprościej jak mogę to wytłumaczyć w inny sposób. Z równania kwadratowego w postaci kanonicznej widać, że wierzchołek paraboli w kierunku x jest przesunięty o -(b/(2*a)) a w kierunku y o -(delta/(4*a)).
Najdokładniej widać to w równaniu jeżeli nie przyrównamy je do zera, wtedy mamy go w ogólnej postaci dla każdego a,b,c, jeżeli teraz przeniesiemy -(delta/(4*a)) na stronę f(x) wtedy te przesunięcia będą wyraźnie widoczne. Pokazuję to na poniższym zdjęciu
Przepraszam za powyższy błąd oczywiście współrzędną x - ową wierzchołka paraboli jest
x = -(b/(2*a)
Długość wektora równania kwadratowego pokazałem na poniższym zdjęciu
Przykład
Znajdź równanie prostej przechodzącej przez miejsce zerowe paraboli oraz przez jej wierzchołek. Równanie kwadratowe podaję na poniższym zdjęciu
Otrzymaliśmy więc poprawne równanie.
Wzory Wieta
Wzory Wieta biorą się po przez kombinację dwóch rozwiazań równania kwadratowego.
x1+ x2
x1*x2
Podstawmy za x1 i x2 rozwiązania powyższe wtedy
Przykład
Wzory Wieta wykorzystuje się do rozwiązywania równań z parametrem. Parametrem jest uzmiennione a , b i c. Rozwiążmy nap takie zadanie.
Dla jakiego parametru m, równanie kwadratowe ma dwa rozwiązania o różnych znakach.
Przykład 2
Dla powyższego zadania znaleźć wektor wodzący wierzchołka paraboli.
Wektor ten jest zaczepiony w początku układu współrzędnych
Na koniec zbierzmy najważniejsze wzory tyczące się równania kwadratowego. Na poniższym zdjęciu drugie równanie to równanie paraboli. Zapamiętajcie, przesunięcia wzdłuż osi x i y, W matematyce geometrycznej to podstawa, spotkacie to przy równaniach okręgu elipsy i tp.
Współrzędne wierzchołka paraboli Ww
na zakończenie f(x) = y trzeba się przyzwyczaić do tych dwóch symboli oznaczających wartości funkcji.
Ogniskowa przestrzeni funkcyjnych
Sam wyprowadziłem ten wzór i pamiętajcie, że mogłem się pomylić.
Ogniskowa to punkt którego prawdopodobieństwo znalezienia wszystkich elementów równa się 100% = 1. Dla przestrzeni funkcyjnych, którą w tym przypadku jest parabola, można wyprowadzić wzór z ciągów liczbowych. Układamy ciąg liczbowy dla liczb nie parzystych 1,3,5,7,9... i parzystych 2,4,6,8... po czym zauwarzamy, że liczby parzyste plus parzyste dają liczby parzysta i neparzyste plus nieparzyste dają też liczby parzyste. Mamy więc dwa ciągi an i bn, które sumujemy. Nie będę tego dowodu tutaj przeprowadzał podam tylko ogólny wynik
Było by to ogólne prawo mówiące, że ogniskowa dowolnej funkcji o ile ona istnieje, leży w odległości jednej trzeciej współrzędnej y licząc od wierzchołka tej funkcji gdzie
Pionowa kreska oznacza przestrzeń afiniczną rozdzielającą dwie przestrzenie
A - przestrzeń wektorowa
B - Przestrzeń skalarna
Za przestrzeń skalarną przyjmujemy jeden, mamy do czynienia z wektorami. Teraz wyobraźmy sobie, że na parabolę puszczamy strumień światła, który skupi nam się w jednym punkcie. jest to punkt 100% prawdopodobieństwa prawdy, czyli możemy podstawić f(x) = 1. Oznacza to, że w tym punkcie na pewno znajdziemy wszystkie promienie.
Podstawienie za x współrzędnej wierzchołka paraboli gwarantuje zaczepienie ogniskowej w tym że wierzchołku, czyli na osi symetrii paraboli.
Jeżeli w takiej ogniskowej umieścimy źródło światła to zajdzie sytuacja odwrotna do poprzedniej, promień światła z takiego reflektora parabolicznego wyjdzie prawie równoległy. Prawie, gdyż źródło światła żarówki nie jest punktowe.
Zwracam jeszcze Waszą szczególną uwagę na fakt, iż planety naszego układu planetarnego najprawdopodobniej krążą po elipsie, a w jednej z ogniskowych tej elipsy znajduje się Słońce. Gdy by powyższy wzór, który wyprowadziliśmy był słuszny, a nie mam podstaw uważać, że nie jest, choć zawsze mogłem się pomylić, wtedy wyznaczając współrzędne wierzchołków tej elipsy mamy gotowy wzór na ogniskową, a tym samym na minimalną odległość planet od Słońca.
Rachunek wektorowy należy traktować jako mocno przybliżony, gdyż jedynka trygonometryczna nie jest spełniona. Jedynka trygonometryczna jest udowodniona pośrednio przez wynikające z niej prawo Pitagorasa, łatwo to sprawdzić wyrysowując sobie kolejne trójkąty prostokątne.
My proponujemy rozwiązać następujący układ równań
Zauważmy, że tangensy są pochodnymi funkcji liniowej przedstawiającej wektory a i b i nie tylko liniowej lecz wszystkich funkcji. W ten sposób otrzymujemy wzór na cosinus konta między dwiema dowolnymi funkcjami. Z wyprowadzeniem sinusa sami już sobie poradzicie. Ogólny zapis wygląda następująco
Rachunek pochodnych znajdziecie tutaj
http//jakpowstajfraktale.blogspot.com
R
Zapraszam do pobierania darmowych korepetycji przez internet z matematyki i fizyki - korepetycji online.